Page 79 - 2025年第56卷第2期

Ｙ＝ Ｔ＋ Ｓ＋ Ｒ （１）
ｔ ｔ ｔ ｔ
式中：Ｙ为 ｔ时刻原始天然径流值；Ｔ为 ｔ时刻的趋势项值；Ｓ为 ｔ时刻的季节项值；Ｒ为 ｔ时刻的残差
ｔ ｔ ｔ ｔ
项值，ｔ ＝ １ ，２，…，Ｎ。
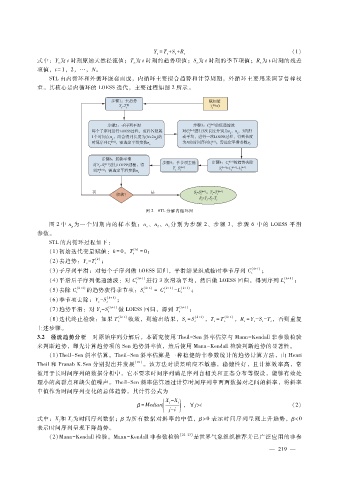
ＳＴＬ由内循环和外循环嵌套而成，内循环主要拟合趋势和计算周期，外循环主要用来调节鲁棒权
重。其核心是内循环的 ＬＯＥＳＳ迭代，主要过程如图 ２所示。

图 ２ ＳＴＬ分解内循环图

图 ２中 ｎ为一 个周 期 内 的 样 本 数；ｎ、ｎ、ｎ分 别 为 步 骤 ２、步 骤 ３、步 骤 ６中 的 ＬＯＥＳＳ平 滑
ｐ ｓ ｌ ｔ
参数。
ＳＴＬ的内循环过程如下：
（ｋ）
（ １）初始迭代变量赋值：ｋ ＝ ０，Ｔ ＝ ０；
ｔ
（ｋ）
（ ２）去趋势：Ｙ－ Ｔ ；
ｔ
ｔ
（３）子序列平滑：对每个子序列做 ＬＯＥＳＳ回归，平滑结果组成临时季节序列 Ｃ （ｋ ＋ １ ） ；
ｔ
（４）平滑后子序列低通滤波：对 Ｃ （ｋ ＋ １） 进行 ３次滑动平均，然后做 ＬＯＥＳＳ回归，得到序列 Ｌ （ｋ ＋ １） ；
ｔ ｔ
（５）去除 Ｃ （ｋ ＋ １ ） 的趋势获得季节项：Ｓ （ｋ ＋ １ ） ＝Ｃ （ｋ ＋ １ ） － Ｌ （ｋ ＋ １ ） ；
ｔ ｔ ｔ ｔ
（ ６）季节项去除：Ｙ－ Ｓ （ｋ ＋ １ ） ；
ｔ ｔ
（ ７）趋势平滑：对 Ｙ－ Ｓ （ｋ ＋ １） 做 ＬＯＥＳＳ回归，得到 Ｔ （ｋ ＋ １） ；
ｔ ｔ ｔ
（８）迭代终止检验：如果 Ｔ （ｋ ＋ １ ） 收敛，则输出结果，Ｓ＝ Ｓ （ｋ ＋ １ ） ，Ｔ＝ Ｔ （ｋ ＋ １ ） ，Ｒ＝ Ｙ－ Ｓ－ Ｔ，否则重复
ｔ ｔ ｔ ｔ ｔ ｔ ｔ ｔ ｔ
上述步骤。
３．２ 径流趋势分析 对原始序列分解后，本研究使用 Ｔｈｅｉｌ － Ｓｅｎ斜率估算与 Ｍａｎｎ － Ｋｅｎｄａｌｌ非参数检验
来判断趋势，即先计算趋势项的 Ｓｅｎ趋势斜率值，然后使用 Ｍａｎｎ － Ｋｅｎｄａｌｌ检验判断趋势的显著性。
（ １）Ｔｈｅｉｌ － Ｓｅｎ斜率估算。Ｔｈｅｉｌ － Ｓｅｎ斜率估算是一种稳健的非参数统计的趋势计算方法，由 Ｈｅｎｒｉ
Ｔｈｅｉｌ 和 ＰｒａｎａｂＫ．Ｓｅｎ分别提出并发展 ［２１］ 。该方法对误差响应不敏感，稳健性好，且计算效率高，常
被用于长时间序列的数据分析中，它不要求时间序列满足序列自相关和正态分布等假设，能够有效处
理小的离群点和缺失值噪声。Ｔｈｅｉｌ － Ｓｅｎ斜率估算通过计算时间序列中两两数据对之间的斜率，将斜率
中值作为时间序列变化的总体趋势。其计算公式为
Ｘ－ Ｘ
( )
ｊ
ｉ
β ＝ Ｍｅｄｉａｎ ｊ － ｉ ，ｊ＞ｉ （２）
式中：Ｘ和 Ｘ为时间序列数据；β 为所有数据对斜率的中值，β ＞０表示时间序列呈现上升趋势，β ＜０
ｊ ｉ
表示时间序列呈现下降趋势。
（２）Ｍａｎｎ － Ｋｅｎｄａｌｌ检验。Ｍａｎｎ － Ｋｅｎｄａｌｌ非参数检验 ［２２ － ２３］ 是世界气象组织推荐并已广泛应用的非参

— ２ １ ９ —