Page 89 - 水利学报2025年第56卷第4期

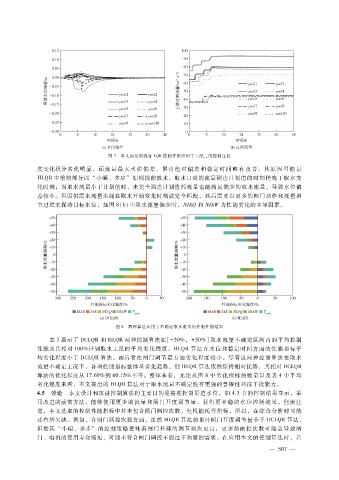
图 ７ 本文前反馈混合 ＬＱＲ控制算法应用于工况二的控制过程
度变化积分劣 化明 显，而 流量 最 大 水 位 偏 差、累 计 绝 对 偏 差 和 稳 定 时 间 略 有 改 善。其 原 因 可 能 是
ＨＬＱＲ中前馈部分以 “小幅、多步” 原则提前放水，取水口处的流量到达计划值的时刻稍晚于取水变
化时刻；当取水流量小于计划值时，未完全到达计划值的流量也能满足偏少的取水流量，导致水位偏
差较小。但因供需水流量未能在取水开始变化时刻就完全匹配，其后需要以更多的闸门动作和流量调
节过程来保持目标水位，如图 ８（ｂ）中取水流量偏少时，ＮＩＡＱ和 ＮＩＡＷ为性能劣化的主导因素。

图 ８ 两种算法应用于不确定取水流量的控制性能结果

表 ３展示了 ＤＣＬＱＲ和 ＨＬＱＲ两种控制算法在［ － ５０％，＋ ５０％］取水流量不确定区间内的平均控制
性能及其相对 １００％计划取水工况的平均劣化程度。ＨＬＱＲ算法在水位和稳定时间方面的性能指标平
均劣化程度小于 ＤＣＬＱＲ算法，而后者在闸门调节量方面劣化程度较小。尽管这两种控制算法在取水
流量不确定工况下，各项性能指标整体呈劣化趋势，但 ＨＬＱＲ算法依然保持相对优势，其相对 ＤＣＬＱＲ
算法的优化程度从 １７．６９％到 ６０．１５％不等。整体来看，无论从图 ８中劣化指标的数量以及表 ４中平均
劣化程度来看，本文提出的 ＨＬＱＲ算法对于取水流量不确定性有更强的鲁棒性和抗干扰能力。
４．５ 讨论 本文设计和改进控制算法的主要目的是精准控制渠道水位，如 ４．３节的控制结果显示，采
用改进的前馈方法，能够使用更少的流量和闸门开度调节量，获得更平稳的水位控制效果。但需注
意，本文选取的控制性能指标中并未包含闸门调控次数、电机能耗等指标，所以，在综合分析时可能
还有所欠缺。例如，在闸门调控次数方面，虽然 ＨＬＱＲ算法的累计闸门开度调节量小于 ＤＣＬＱＲ算法，
但是其 “小幅、多步” 的控制策略意味着闸门升降的调节频次更高，更多的闸控次数可能会导致闸
门、电机的使用寿命缩短，可能不符合闸门调控不能过于频繁的需求。在应用本文的控制算法时，若

— ５ ０ ７ —