Page 107 - 2025年第56卷第6期

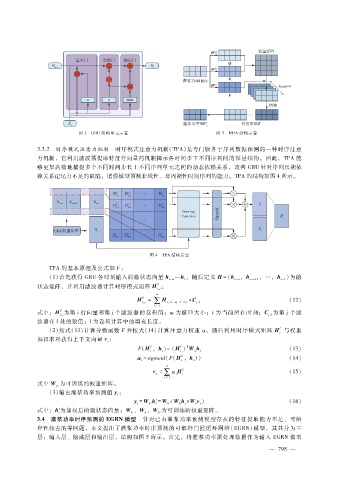
图 ２ ＧＲＵ结构单元示意 图 ３ ＭＨＡ结构示意

３．３．２ 时序模式注意力机制 时序模式注意力机制（ＴＰＡ）是专门服务于序列数据预测的一种时序注意
力机制，它利用滤波器提取特征行向量的机制揭示各时间步下不同序列间的深层结构。因此，ＴＰＡ能
够更加高效地捕捉多个不同时间步长上不同序列单元之间的动态依赖关系，改善 ＧＲＵ针对序列长期依
赖关系记忆力不足的缺陷，增强模型预测非线性、非周期性时间序列的能力。ＴＰＡ的结构如图 ４所示。

图 ４ ＴＰＡ结构示意
ＴＰＡ的基本原理及公式如下：
（ １）首先获得 ＧＲＵ各时刻输入的隐状态向量 ｈ —ｈ，随后定义 Ｈ＝ （ｈ ，ｈ ｔ － ω ＋ １ ，…，ｈ ）为隐
ｔ
ｔ － ω
ｔ － １
ｔ － ω
Ｃ
状态矩阵，并利用滤波器计算时序模式矩阵 Ｈ ：
ｉ ，ｊ
ω
Ｃ
Ｈ ＝ Ｈ ｉ，（ｔ － ω－ １ ＋ ｌ） × Ｃ ｊ，ｌ （１２）
ｉ，ｊ ∑
ｌ ＝１
Ｃ
式中：Ｈ 为第 ｉ行向量和第 ｊ个滤波器的卷积值；ω为窗口大小；ｔ为当前所在时刻；Ｃ 为第 ｊ个滤
ｉ，ｊ
ｊ，ｌ
波器在 ｌ处的数值；ｌ为卷积计算中的填充长度。
Ｃ
（２）按式（１３）计算分数函数 Ｆ并按式（１４）计算注意力权重 α ，随后利用时序模式矩阵 Ｈ 与权重
ｉ
加权求和获得上下文向量 ｖ：
ｔ
Ｃ
Ｔ
Ｃ
Ｆ（Ｈ ，ｈ） ＝（Ｈ ）Ｗ ｈ （１３）
ｉ ｔ ｉ ａ ｔ
Ｃ
＝ ｓｉｇｍｏｉｄ（Ｆ（Ｈ ，ｈ）） （１４）
α ｉ ｉ ｔ
ｎ
ｔ ∑
ｖ ＝ α ｉ Ｈ Ｃ （１５）
ｉ
ｉ ＝１
式中 Ｗ 为可训练的权重矩阵。
ａ
（ ３）输出灌浆功率预测值 ｙ：
ｔ
ｙ＝ Ｗ ｈ′ ＝ Ｗ （Ｗ ｈ＋ Ｗ ｖ） （１６）
ｖ ｔ
ｔ
ｈ′ ｔ
ｈ′
ｈ ｔ
式中：ｈ′为加权后的隐状态向量；Ｗ 、Ｗ 、Ｗ 为可训练的权重矩阵。
ｔ ｈ ｖ ｈ′
３．４ 灌浆功率时序预测的 ＥＧＲＮ模型 针对已有灌浆功率预测模型存在的特征提取能力不足、可解
释性较差的等问题，本文提出了灌浆功率时序预测的可解释门控循环网络（ ＥＧＲＮ）模型，其共分为三
层：输入层、隐藏层和输出层，结构如图 ５所示。首先，将灌浆功率预处理数据作为输入 ＥＧＲＮ模型
— ７ ９ ５ —