Page 110 - 2025年第56卷第6期

４．３ 可解释性分析 本文融合了 ＭＨＡ和 ＴＰＡ两种注意力机制，分别从频率与时间两个维度进行分
析。通过 ＣＥＥＭＤＡＮ分解获得灌浆功率的 ＩＭＦｓ，从频率特征与时序特征表述灌浆功率的动态变化规
律，客观地表征了灌浆功率随时间演变的多元模式和特性。
４．３．１ 频率特征分析 通过引入 ＭＨＡ评估每个 ＩＭＦｓ的重要性并为其赋予相应的关注度，提升了模型
对频率特征的筛选与聚合能力。这一过程不仅强化了模型对灌浆功率变化细节的捕捉能力，而且揭示
了各个频率的 ＩＭＦｓ在灌浆功率预测中的相对重要性。
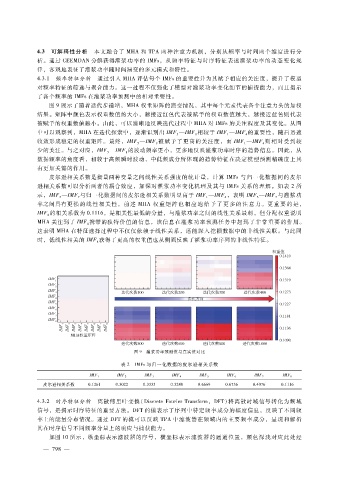
图 ９展示了随着迭代步递增，ＭＨＡ权重矩阵的演变情况，其中每个元素代表各个注意力头的加权
结果。矩阵中颜色表示权重数值的大小，越接近红色代表被赋予的权重数值越大，越接近蓝色则代表
被赋予的权重数值越小。由此，可以清晰地反映迭代过程中 ＭＨＡ对 ＩＭＦｓ的关注程度及其变化。从图
中可以观察到，ＭＨＡ在迭代探索中，逐渐识别出 ＩＭＦ—ＩＭＦ相较于 ＩＭＦ—ＩＭＦ的重要性，随后迅速
１
４
５
８
收敛形成稳定的权重矩阵。最终，ＩＭＦ—ＩＭＦ被赋予了更高的关注度，而 ＩＭＦ—ＩＭＦ则相对受到较
４
１
５
８
少的关注。与之对应，ＩＭＦ—ＩＭＦ的波动频率更小，更多地反映灌浆功率时序的趋势信息。因此，从
５ ８
数据频率的角度看，相较于高频瞬时波动，中低频成分所体现的趋势特征在决定模型预测精确度上具
有更加关键的作用。
皮尔逊相关系数是衡量两种变量之间线性关系强度的统计量，计算 ＩＭＦｓ与归一化数据间的皮尔
逊相关系数可以分析两者的耦合效应，加深对灌浆功率变化机理及其与 ＩＭＦｓ关系的理解。如表 ２所
示，ＩＭＦ—ＩＭＦ与归一化数据间的皮尔逊相关系数明显高于 ＩＭＦ—ＩＭＦ，表明 ＩＭＦ—ＩＭＦ与灌浆功
１
７
５
７
４
５
率之间具有更 强的 线性相 关性，前述 ＭＨＡ权重矩阵 也 相 应 地 给 予 了 更 多 的 注 意 力。更 重 要 的 是，
ＩＭＦ的相关系数为 ０．１１１６，是相关性最低的分量，与灌浆功率之间的线性关系最弱。但分配权重说明
８
ＭＨＡ关注到了 ＩＭＦ携带的独特价值的信息，该信息在灌浆功率预测任务中起到了非常重要的作用。
８
这表明 ＭＨＡ在特征选择过程中不仅仅依赖于线性关系，还能深入挖掘数据中的非线性关联。与此同
时，低线性相关的 ＩＭＦ获得了更高的权重值也从侧面反映了灌浆功率序列的非线性特征。
８

图 ９ 灌浆功率预测值与真实值对比

表 ２ ＩＭＦｓ与归一化数据的皮尔逊相关系数
ＩＭＦ １ ＩＭＦ ２ ＩＭＦ ３ ＩＭＦ ４ ＩＭＦ ５ ＩＭＦ ６ ＩＭＦ ７ ＩＭＦ ８
皮尔逊相关系数 ０．１２６１ ０．３０２２ ０．３３３３ ０．３２４８ ０．６６６９ ０．６７３６ ０．４０７６ ０．１１１６

４．３．２ 时序特征分析 离散傅里叶变换（ＤｉｓｃｒｅｔｅＦｏｕｒｉｅｒＴｒａｎｓｆｏｒｍ，ＤＦＴ）将离散时域信号转化为频域
信号，是揭示时序特征的重要方法。ＤＦＴ的模表示了序列中特定频率成分的幅度信息，反映了不同频
率上的能量分布情况。通过 ＤＦＴ的模可以反映 ＴＰＡ中滤波器在频域内的主要频率成分，呈现和解析
其在时序信号不同频率分量上的响应与捕获能力。
如图 １０所示，纵坐标表示滤波器的序号，横坐标表示滤波器的通道位置，颜色深浅对应此处经

— ７ ９ —
８