Page 53 - 2025年第56卷第6期

径之比，根据挟沙水流连续原理得出：
Q/M = R U （8）
2
( ) -0.35
Q
J = 0.00526S v M （9）
( ) 0.45
Q
-0.15 （10）
R = 0.546S v M
式中要确定河相关系三个未知量 R、J、B 与来水来沙函数关系，还需要补充一个方程才能求解，
而对非漫滩水流，可采用阿尔图宁稳定河宽公式 B = AQ /J ，系数 A 经黄河下游资料拟合分析后为
0.5
0.2
0.24 。显然，以上三式联立并整理可得到新的黄河下游河相关系：
A = 4.2S v
-0.289 Q 0.364 （11）
R = 0.058S v
J = 0.03S v Q -0.284 （12）
1.10
B = 8.47S v Q 0.557 （13）
0.02
2.2 新河相关系的验证 联立求解步骤详见文献［1，6］。选择具有代表性的 1977 年黄河下游高含沙洪
水过程验证新河相关系式（11）—（13）。以花园口、夹河滩测站为例，实测含沙量体积比 S = 0.0026 ~
v
0.1753，流量 Q = 860 ~ 8783 m /s，过水面积 A = 841.08 ~ 8783 m ，比降 J = 0.000 085 ~ 0.000 38。将新河
2
3
相关系式（11）—（13）的计算结果与钱宁等 ［12］ 、江恩慧等 ［13］ 学者所提出的黄河下游河相关系给出的结
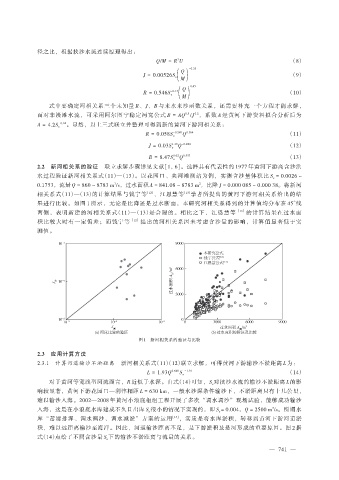
果进行比较。如图 1 所示，无论是比降还是过水断面，本研究河相关系得到的计算值均分布在 45°线
两侧，表明新建的河相关系式（11）—（13）是合理的。相比之下，江恩慧等 ［13］ 的计算结果在过水面
积比较大时有一定偏差；而钱宁等 ［12］ 提出的河相关系因未考虑含沙量的影响，计算值显著低于实
测值。

图 1 新河相关系的验证与比较

2.3 应用计算方法
2.3.1 计算河道输沙不淤距离 新河相关系式（11）（12）联立求解，可得黄河下游输沙不淤距离 L 为：
L = 1.93Q 0.648 S v -1.39 （14）
对于黄河等宽浅型河流而言，R 近似于水深。由式（14）可知，S 对挟沙水流的输沙不淤距离 L 的影
v
响较显著，黄河下游花园口—利津相距 L = 630 km，一般水沙深条件输沙下，不淤距离只有十几公里，
难以输沙入海。2002—2008 年黄河小浪底枢组工程开展了多次“调水调沙”现场试验，能够成功输沙
入海，这是在小浪底水库建成不久且出库 S 很小的情况下实现的，即 S = 0.004，Q = 2500 m /s。所谓水
3
v
v
库“蓄清排浑、调水调沙、调水减淤”方案的运用 ［14］ ，实质是将水库淤积，转移到黄河下游河道淤
积，难以远距离输沙至海洋。因此，河道输沙距离不足，是下游淤积及悬河形成的重要原因。图 2 据
式（14）点绘了不同含沙量 S 下的输沙不淤距离与流量的关系。
v
— 741 —