Page 61 - 2025年第56卷第6期

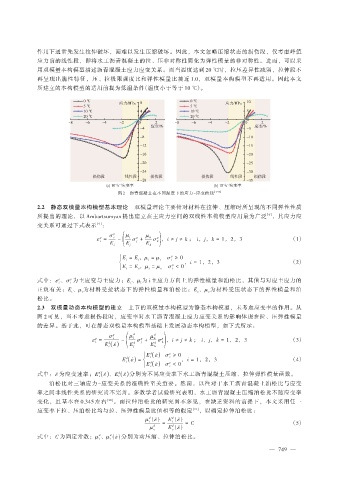
作用下通常先发生拉伸破坏，而难以发生压缩破坏。因此，本文忽略压缩状态的损伤段，仅考虑峰值
应力前的线性段，即将水工沥青混凝土的拉、压非对称性简化为弹性模量的非对称性。进而，可以采
用双模量本构模型描述沥青混凝土应力应变关系。而当温度达到 20 ℃时，拉压差异性减弱，拉伸段不
再呈现出脆性特征，压、拉极限强度比和弹性模量比接近 1.0，双模量本构模型不再适用。因此本文
所建立的本构模型的适用前提为低温条件（温度小于等于 10 ℃）。

图 2 沥青混凝土在不同温度下的应力-应变曲线 ［7-8］

2.2 静态双模量本构模型基本理论 双模量理论主要针对材料在拉伸、压缩时所呈现的不同弹性性质
所提出的理论，以 Ambartsumyan 提出建立在主应力空间的双线性本构模型应用最为广泛 ，其应力应
［9］
［9］
变关系可通过下式表示 ：
p E k )
p σ i μ j p μ k p
ε i = - σ j + σ k ，i ≠ j ≠ k ； i，j，k = 1，2，3 （1）
E i ( E j
p
ìE i = E t ，μ i = μ t σ i ≥ 0
í p ，i = 1，2，3 （2）
î E i = E c ，μ i = μ c σ i < 0
p
p
式中：ε i 、σ i 为主应变与主应力；E 、μ 为 i 主应力方向上的弹性模量和泊松比，其值与对应主应力的
i
i
正负有关；E 、μ 为材料受拉状态下的弹性模量和泊松比；E 、μ 为材料受压状态下的弹性模量和泊
t t c c
松比。
2.3 双模量动态本构模型的建立 上节的双模量本构模型为静态本构模型，未考虑应变率的作用。从
图 2 可见，当不考虑损伤段时，应变率对水工沥青混凝土应力应变关系的影响体现在拉、压弹性模量
的差异。基于此，可在静态双模量本构模型基础上发展动态本构模型，如下式所示：
p d E k )
d
p σ i μ j p μ k p
ε i = d - d σ j + d σ k ，i ≠ j ≠ k ； i，j，k = 1，2，3 （3）
E i( ) ε ̇ ( E j
d p
ìE t( ) ε ̇ σ i ≥ 0
d
E i( ε ̇ ) = í d p ，i = 1，2，3 （4）
î E c( ) ε ̇ σ i < 0
d
d
式中：ε ̇ 为应变速率；E c( ε ̇ )、E t( ε ̇ ) 分别为不同应变率下水工沥青混凝土压缩、拉伸弹性模量函数。
泊松比对三轴应力-应变关系的准确性至关重要。然而，以往对于水工沥青混凝土泊松比与应变
率之间非线性关系的研究尚不完善。多数学者试验研究表明，水工沥青混凝土压缩泊松比不随应变率
变化，且基本在 0.345 左右 ［20］ 。而拉伸泊松比的研究尚不多见，在缺乏资料的前提下，本文采用任一
应变率下拉、压泊松比均与拉、压弹性模量比值相等的假定 ［21］ ，以确定拉伸泊松比：
d d
μ t (ε ̇ ) E t (ε ̇ )
= = C （5）
d d
μ c E c (ε ̇ )
d
d
式中：C 为固定常数；μ c 、μ t (ε ̇ ) 分别为动压缩、拉伸泊松比。
— 749 —