Page 64 - 2025年第56卷第6期

p p p p p 2 p p p 2
σ i - σ j ε i (E i - E j C ) - ε j (E j - E i C )
= （19）
p p p p p p
2
2(ε i - ε j ) 2(ε i - ε j )(1 - E i E j C )
正确判断应力状态是求解双模量问题及提高收敛速率的关键。以往针对应力状态判断的高效算法
多采用试算法 ［16-17］ ，即通过假定材料的应力状态，计算对应的刚度矩阵，并利用该刚度矩阵求解试算
应力，再将试算结果与假定结果进行对比，若两者一致，则判断应力状态正确。然而，此类方法依赖
于刚度矩阵的构建，但刚度矩阵的建立需先确定拉、压弹性模量。而由式（6）—（9）可知拉压弹性模量
的确定取决于应变率。此外，由式（12）可知，等效应变率的计算依赖于应力信息，而计算应力时需先
准确判断应力状态。因此，应力状态判断、拉压弹性模量确定以及等效应变率计算三者之间存在耦合
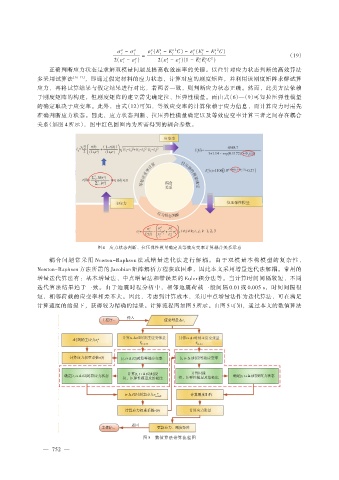
关系（如图 4 所示），图中红色圆圈内为所需得到的耦合参数。

图 4 应力状态判断、拉压弹性模量确定及等效应变率计算耦合关系示意
耦 合 问 题 常 采 用 Newton-Raphson 法 或 增 量 迭 代 法 进 行 解 耦 。 由 于 双 模 量 本 构 模 型 的 复 杂 性 ，
Newton-Raphson 方法所需的 Jacobian 矩阵解析方程获取困难，因此本文采用增量迭代法解耦。常用的
增量迭代算法有：基本增量法、中点增量法和带误差的 Euler 积分法等。当计算时间间隔较短，不同
迭代算法结果趋于一致。由于地震时程分析中，相邻地震荷载一般间隔 0.01 或 0.005 s，时间间隔很
短，相邻荷载的应变率相差不大。因此，考虑到计算成本，采用中点增量法作为迭代算法，可在满足
计算速度的前提下，获得较为精确的结果。计算流程图如图 5 所示。由图 5 可知，通过本文的数值算法

图 5 数值算法计算流程图

— 752 —