Page 68 - 2025年第56卷第6期

表 4 不同时刻心墙特征点 A 的动主应力、瞬时拉压模量及等效应变率
应力/kPa 拉伸弹性模量× 压缩弹性模量×
时间 计算工况 等效应变率/s -1
3
3
10 /kPa 10 /kPa
σ 1 σ 2 σ 3
本文模型 12.8 -7.7 -158.6 397.4 575.0 5.4×10 -4
t=5.00 s
准静态单模量模型 17.4 -8.9 -59.3 171.5 171.5 1.7×10 -4
t =9.27 s 本文模型 145.4 11.4 -7.2 514.5 1221.7 4.4×10 -3
1
t =9.29 s 准静态单模量模型 124.2 9.6 -30.7 171.5 171.5 4.3×10 -3
2
t =7.18 s 本文模型 28.0 -15.3 -491.4 512.1 1201.5 4.3×10 -3
3
t =7.17 s 准静态单模量模型 18.2 -9.6 -140.7 171.5 171.5 4.5×10 -3
4
本文模型 13.2 -6.5 -288.2 447.6 786.5 1.3×10 -3
t=10.00 s
准静态单模量模型 13.0 2.9 -92.6 171.5 171.5 1.5×10 -3
本文模型 11.2 -30.9 -193.9 437.8 739.1 1.1×10 -4
t=15.00 s
准静态单模量模型 13.3 -28.4 -80.5 171.5 171.5 5.1×10 -4
本文模型 1.6 0.9 -10.2 333.3 394.7 1.8×10 -4
t=20.00 s
准静态单模量模型 1.2 -1.8 -4.7 171.5 171.5 2.2×10 -4

注：t 、t 分别为本文模型和准静态单模量模型最大主拉应力出现时刻；t 、t 分别为本文模型和准静态单模量模型最大主压应力出现
1 2 3 4
时刻。

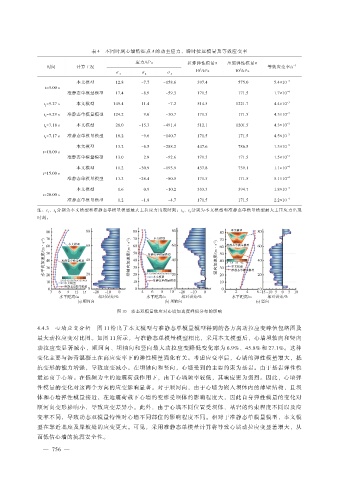
图 10 动态双模量效应对心墙加速度峰值分布的影响

4.4.3 心墙应变分析 图 11 给出了本文模型与准静态单模量模型得到的各方向动拉应变峰值包络图及

最大动拉应变对比图。如图 11 所示，与准静态单模量模型相比，采用本文模型后，心墙坝轴向和竖向
动拉应变显著减小，顺河向、坝轴向和竖向最大动拉应变降低变化率为 6.9%、45.8% 和 27.1%。这种
变化主要与沥青混凝土在高应变率下的弹性模量强化有关。考虑应变率后，心墙的弹性模量增大，抵
抗变形的能力增强，导致应变减小。在坝轴向和竖向，心墙受到的主要约束为基岩。由于基岩弹性模
量远高于心墙。在低频为主的地震荷载作用下，由于心墙频率较低，其响应更为强烈。因此，心墙弹
性模量的变化对这两个方向的应变影响显著。对于顺河向，由于心墙为嵌入坝体内的薄壁结构，且坝
体和心墙弹性模量接近，在地震荷载下心墙的变形受坝体的影响程度大，因此自身弹性模量的变化对

顺河向变形影响小，导致应变差异小。此外，由于心墙不同位置受坝体、基岩的约束程度不同以及应
变率不同，导致动态双模量特性对心墙不同部位的影响程度不同。相对于准静态单模量模型，本文模
型在靠近基座及岸坡处的应变更大。可见，采用准静态单模量计算将导致心墙动拉应变显著增大，从
而低估心墙的抗震安全性。

— 756 —