Page 67 - 2025年第56卷第6期

采用 Duncan-Chang E-B 模型 ［22-23］ 作为堆石体、过渡层材料的静力本构模型，采用沈珠江修正的等
效线性黏弹性模型 ［24］ 作为堆石体和过渡层材料的动力本构模型，具体参数见表 3。基岩和混凝土采用
线弹性模型，基岩的密度、弹性模量和泊松比分别为 2.70 g/cm 、8 GPa 和 0.24，混凝土的密度、弹性
3
模量和泊松比分别为 2.16 g/cm 、28 GPa 和 0.167。
3
表 3 坝体材料静、动力材料参数
静力参数 动力参数
材料
ρ/（g/cm ） K n R c/kPa φ/ （°） P K m K /K k k n ν λ
3
f a b ur 1 2 max
堆石 2.15 750 0.60 0.78 0 42 100 700.0 0.10 2 20.0 2270 0.273 0.35 0.22
过渡层 2.25 910.9 0.31 0.63 0 50.6 100 395.5 0.34 1.5 28.3 1832 0.375 0.328 0.22

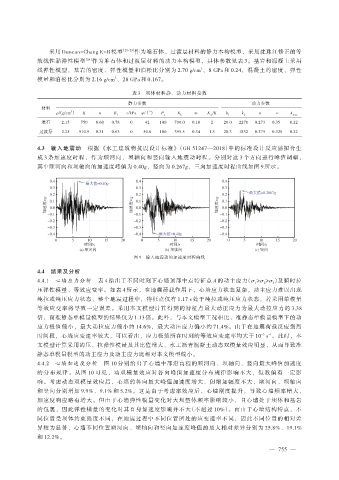
4.3 输入地震动 根据 《水工建筑物抗震设计标准》（GB 51247—2018）中的标准设计反应谱拟合生
成 3 条加速度时程，作为顺河向、坝轴向和竖向输入地震动时程。分别对这 3 个方向进行峰值调幅，
其中顺河向和坝轴向的加速度峰值为 0.40g，竖向为 0.267g，三向加速度时程曲线如图 9 所示。

图 9 输入地震动的加速度时程曲线

4.4 结果及分析
4.4.1 心墙应力分析 表 4 给出了不同时刻下心墙顶部中点特征点 A 的动主应力（σ ≥σ ≥σ ）及瞬时拉
1 2 3
压弹性模量、等效应变率。如表 4 所示，在地震荷载作用下，心墙应力状态复杂，动主应力难以出现
纯拉或纯压应力状态，整个地震过程中，特征点仅有 1.17 s 处于纯拉或纯压应力状态，若采用单模量
等效应变率将导致一定误差。采用本文模型计算得到的特征点最大动压应力为最大动拉应力的 3.38
倍，而准静态单模量模型的结果仅为 1.13 倍。此外，与本文模型工况相比，准静态单模量模型下的动
应力极值偏小，最大动拉应力偏小约 14.6%，最大动压应力偏小约 71.4%。由于在地震荷载反应强烈
时间段，心墙应变速率较大，可以看出，应力极值所在时刻的等效应变速率均大于 10 s 。此时，本
-1
-3
文模型计算采用的压、拉弹性模量及其比值增大，水工沥青混凝土动态双模量效应明显，从而导致准
静态单模量模型的动主应力及动主应力比相对本文模型偏小。
4.4.2 心墙加速度分析 图 10 分别给出了心墙中部沿高程的顺河向、坝轴向、竖向最大峰值加速度
的分布规律。从图 10 可见，动双模量效应对各向峰值加速度分布规律影响不大，但数值有一定影
响。考虑动态双模量效应后，心墙的各向最大峰值加速度增大，但增加幅度不大，顺河向、坝轴向
和竖向分别增加 9.9%、9.1% 和 5.2%。这是由于考虑率效应后，心墙刚度提升，导致心墙频率增大，
加速度响应略有增大。但由于心墙弹性模量变化对大坝整体频率影响较小，且心墙处于坝体和基岩
的包裹，因此弹性模量的变化对其自身加速度影响并不大（不超过 10%）。而由于心墙结构特点，不
同位置受坝体约束强度不同，在地震过程中不同位置所处的应变速率不同，因此不同位置的相对差

异较为显著，心墙不同位置顺河向、坝轴向和竖向加速度峰值的最大相对差异分别为 25.8%、19.1%
和 12.2%。

— 755 —