Page 63 - 2025年第56卷第6期

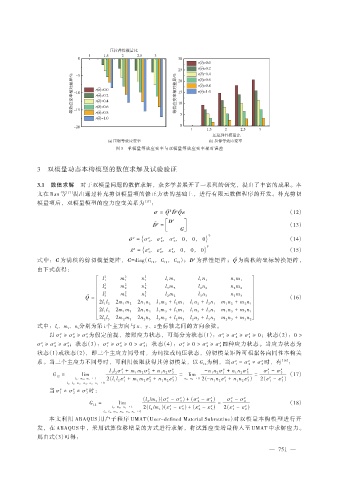
图 3 单模量等效应变率与双模量等效应变率相对误差

3 双模量动态本构模型的数值求解及试验验证

3.1 数值求解 对于双模量问题的数值求解，众多学者展开了一系列的研究，提出了丰富的成果。本
文在 Ran 等 ［17］ 提出通过补充剪切模量项的修正方法的基础上，进行有限元数值程序的开发。补充剪切
模量项后，双模量模型的应力应变关系为 ［17］ ：
͂ T ͂ p ͂
σ = Q D Qε （12）
ê ê
D = ê é D p ù ú ú ú ú （13）
ê
͂ p
ë G û
σ ͂ = {σ 1 ， σ 2 ， σ 3 ， 0， 0， 0} T （14）
p
p
p
p
ε ͂ = {ε 1 ， ε 2 ， ε 3 ， 0， 0， 0} T （15）
p
p
p
p
p
͂
式中：G 为满秩的剪切模量矩阵，G=diag（G ，G ，G ）；D 为弹性矩阵；Q 为满秩的坐标转换矩阵，
12 13 23
由下式获得：
ê ê é l 1 2 m 1 2 n 1 2 l 1 m 1 l 1 n 1 n 1 m 1 ù ú ú
2 2 2 ú ú
ê ê l 2 m 2 n 2 l 3 m 3 l 2 n 2 n 2 m 2
ê ê 2 2 2 ú ú
Q = ê ê l 3 m 3 n 3 l 2 m 2 l 3 n 3 n 3 m 3 ú ú （16）
͂
ê ê2l 1 l 2 2m 1 m 2 2n 1 n 2 l 1 m 2 + l 2 m 1 l 1 n 2 + l 2 n 1 m 1 n 2 + m 2 n 1 ú ú
ê ê ú ú
ê ê 2l 1 l 3 2m 1 m 3 2n 1 n 3 l 1 m 3 + l 3 m 1 l 1 n 3 + l 3 n 1 m 1 n 3 + m 3 n 1 ú ú
û
ë2l 2 l 3 2m 2 m 3 2n 2 n 3 l 3 m 2 + l 2 m 3 l 2 n 3 + l 3 n 2 m 2 n 3 + m 3 n 2
式中：l 、m 、n 分别为第 i 个主方向与 x、y、z 坐标轴之间的方向余弦。
i
i
i
p p p p p p
以 σ 1 ≥ σ 2 ≥ σ 3 为假定前提，按照应力状态，可划分为状态（1）：σ 1 ≥ σ 2 ≥ σ 3 ≥ 0；状态（2）：0 >
p
p
p
p
p
p
p
p
p
σ 1 ≥ σ 2 ≥ σ 3 ；状态（3）：σ 1 ≥ σ 2 ≥ 0 > σ 3 ；状态（4）：σ 1 ≥ 0 > σ 2 ≥ σ 3 四种应力状态。当应力状态为
状态（1）或状态（2），即三个主应力同号时，为纯拉或纯压状态，剪切模量矩阵可根据各向同性本构关
p
p
p
系。当三个主应力不同号时，可利用极限获得其剪切模量，以 G 为例，当 σ 1 = σ 2 ≠ σ 3 时，有 ［16］ ：
12
p p p p p p p
l 1 l 2 σ 1 + m 1 m 2 σ 2 + n 1 n 2 σ 3 -n 1 n 2 σ 1 + n 1 n 2 σ 3 σ 1 - σ 3
G 12 = lim p p p = lim p p = p p （17）
l 1 ，m 2 ，n 3 → 1 2(l 1 l 2 ε 1 + m 1 m 2 ε 2 + n 1 n 2 ε 3 ) n 1 ，n 2 → 0 2(-n 1 n 2 ε 1 + n 1 n 2 ε 3 ) 2(ε 1 - ε 3 )
l 2 ，l 3 ，m 1 ，m 3 ，n 1 ，n 2 → 0
p
p
p
当 σ 1 ≠ σ 2 ≠ σ 3 时：
p p p p p p
(l 2 /m 1 )(σ 1 - σ 3 ) + (σ 2 - σ 3 ) σ 1 - σ 2
G 12 = lim p p p p = p p （18）
l 1 ，m 2 ，n 3 → 1 2(l 2 /m 1 )(ε 1 - ε 3 ) + (ε 2 - ε 3 ) 2(ε 1 - ε 2 )
l 2 ，l 3 ，m 1 ，m 3 ，n 1 ，n 2 → 0
本文利用 ABAQUS 用户子程序 UMAT（User-defined Material Subroutine）对双模量本构模型进行开
发，在 ABAQUS 中，采用试算位移增量的方式进行求解，将试算应变增量传入至 UMAT 中求解应力。
则由式（3）可得：
— 751 —