Page 60 - 2021年第52卷第7期

方面具有统计意义上的有效性。
4.2 溯源重构序列的分布特征 分布特征是随机

变量取值特性的完整描述，是研究随机现象的核
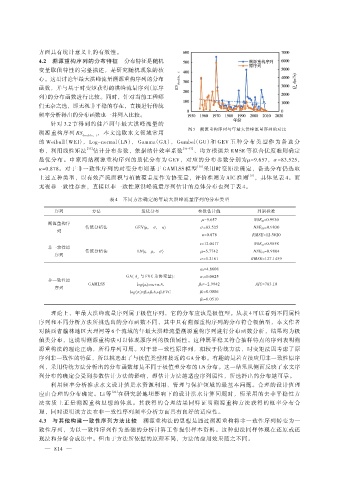
心。这里讨论年最大洪峰流量溯源重构序列的分布 RS double，t
函数，并与基于时变矩获得的洪峰流量序列（原序
列）的分布函数进行比较。同时，针对当前工程师
们无奈之选，即无视非平稳的存在，直接进行传统
频率分析得出的分布函数也一并列入比较。
针对 3.2 节得到的佳芦河年最大洪峰流量的
溯源重构序列 RS double，t ，本文选取水文领域常用 图 5 溯源重构序列与年最大洪峰流量序列的对比
的 Weibull（WEI）， Log-normal（LN）， Gamma（GA）， Gumbel（GU）和 GEV 五 种 分 布 类 型 作 为 备 选 分
布，利用线性矩法 ［35］ 估计分布参数，依据纳什效率系数 ［36-37］ 、均方根误差 RMSE 等拟合优度准则确定
最优分布。申家湾站溯源重构序列的最优分布为 GEV，对应的分布参数分别为μ=9.657，σ=83.525，
κ=0.878。对于非一致性序列的时变分布则基于 GAMLSS 模型 ［38］ 采用时变矩法确定，备选分布仍选取
上述五种类型，以有效产流面积与植被覆盖度作为协变量，评价准则为 AIC 准则 ［39］ ，具体见表 4。而
无视非一致性存在，直接以非一致性原洪峰流量序列估计的总体分布也列于表 4。

表 4 不同方法确定的年最大洪峰流量序列的分布类型
序列 方法 最优分布 参数估计值 判别标准
μ=9.657 NSE pp=0.9930
溯源重构序
传统分析法 GEV(μ, σ, κ) σ=83.525 NSE QQ=0.9830
列
κ=0.878 RMSE=12.5020
z=12.0417 NSE pp=0.9858
非一致性原
传统分析法 LN(z, μ, σ) μ=5.7742 NSE QQ=0.9804
序列
σ=1.2161 RMSE=127.1459
α 0=4.8608
GA( A 与 FVC 为协变量): α 1=0.0025
e
非一致性原
GAMLSS log(μ t)=α 0+α 1A e β 0=-2.9942 AIC=783.10
序列
log(σ t)=β 0+β 1A e+β 2FVC β 1=0.0006
β 2=0.0510
理论上，年最大洪峰流量序列属于极值序列，它的分布应该是极值型。从表 4 可以看到不同属性
序列和不同分析方法所挑选出的分布函数不同，其中只有溯源重构序列的分布符合极值型，本文作者
对陕西省榆林地区大理河等 6 个流域的年最大洪峰流量溯源重构序列进行分布函数分析，结果均为极
值类分布，这说明溯源重构法可以体现原序列的极值属性。这种既平稳又符合抽样特点的序列表明溯
源重构法的理论正确，所得序列可用。对于非一致性原序列，相较于传统方法，时变矩法因考虑了原
序列非一致性的特征，所以挑选出了与极值类型相接近的 GA 分布。有趣的是若直接应用非一致性原序
列，采用传统方法分析出的分布函数却是不同于极值型分布的 LN 分布。这一结果从侧面反映了水文序
列分布的确定会受到参数估计方法的影响，即估计方法越适应序列属性，所选择出的分布越可靠。
利用频率分析推求水文设计值是水资源利用、管理与保护领域的最基本问题。合理的设计值理
应由合理的分布确定。Li 等 ［22］ 在研究淤地坝影响下的设计洪水计算问题时，所采用的去非平稳性方
法实质上正是溯源重构思想的体现。其获得的合理结果同样证明溯源重构方法获得的概率分布合
理，同时说明该方法在非一致性序列频率分析方面具有良好的适应性。
4.3 与其他构建一致性序列方法比较 溯源重构法的思想是通过溯源重构将非一致性序列转变为一

致性序列，为以一致性序列作为基础的分析计算工作提供样本资料。这种想法同样体现在还原或还
现法和分解合成法中。但由于方法所依据的原理不同，方法的应用效果随之不同。
— 814 —