Page 120 - 2021年第52卷第10期

2.4.1 降水发生模型 降水的发生常用链相关的马尔可夫过程来模拟，马尔可夫过程的复杂程度由
其状态数和阶数决定，状态数和阶数越多，模型就越复杂。研究表明一阶的马尔可夫链能够同高阶
模型一样，可很好地描述降水发生等统计特征，已广泛应用于降水发生模拟 ［38-39］ 。本文选用一阶—两
态的马尔可夫链来模拟重现降水发生。在一阶马尔可夫链中，第 t+1 日降水状态的概率仅取决于前一
日 t 的降水状态，降水的发生概率有两种情况：

p = P { X = | 1 X = （9）
01 t + 1 t } 0
p = P { X = | 1 X = } 1 （10）
11 t + 1 t
式中：p 为非雨日之后发生降水的条件概率，p 为雨日之后发生降水的条件概率，可用条件概率公
01 11
式进行计算；X 为第 t 日的降水状态，1 和 0 分别代表发生降水和不发生降水。
t
2.4.2 随机模拟过程 采用一阶—两态的马尔可夫模型随机生成降水发生过程，通过线性矩法估计
实测降水序列对于不同概率分布的参数，用于确定概率分布的分位函数；采用均匀分布函数在［0，
1］区间产生相应站点雨日长度的随机数，作为降水量的频率值；通过概率分布的分位函数计算相应
频率下的分位数，获取随机模拟的降水序列，重复以上步骤 1000 次（具体过程详见参考文献［38］）。
以模拟值 50%、75%、99%、99.9%的分位点和年降水总量标准差（STD）分别代表日降水量序列的低
值、中值、高值、极值以及年际波动情况，最后按照公式（11）计算模拟值和实测值的偏差来评价概
率分布模型的性能。
é
%Bias = 100 ( P - E [P ) ] P ù （11）
ë Obs Sim Obs û
式中： P Obs 为雨日序列各分位处及年降水量标准差的实测值； P Sim 为雨日序列各分位点及年降水量
标准差的模拟值。

3 结果和分析

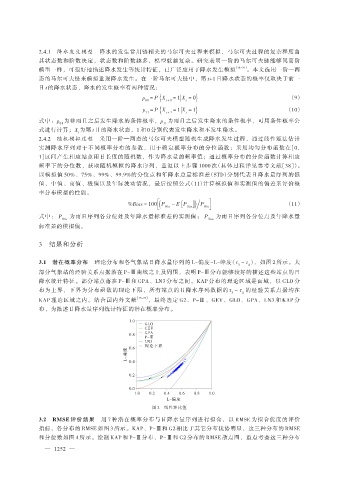
3.1 潜在概率分布 理论分布和各气象站日降水量序列的 L-偏度~L-峰度（τ ~ τ ），如图 2 所示。大
3 4
部分气象站的经验关系点据落在 P-Ⅲ曲线之上及周围，表明 P-Ⅲ分布能够较好的描述这些站点的日
降水统计特征。部分站点落在 P-Ⅲ和 GPA、LN3 分布之间。KAP 分布的理论区域是面域，以 GLO 分
布为上界，下界为分布函数的理论下限，所有站点的日降水序列数据的 τ ~ τ 的经验关系点据均在
3 4
KAP 理论区域之内。结合国内外文献 ［15-25］ ，最终选定 G2、P-Ⅲ、GEV、GLO、GPA、LN3 和 KAP 分
布，为描述日降水量序列统计特征的潜在概率分布。

1.0
GLO
GEV
GPA
0.8
P-Ⅲ
LN3
理论下界
0.6
L-峰度 0.4

0.2

0.0
1.0 0.2 0.4 0.6 0.8 1.0
L-偏度
图 2 线性矩比值
3.2 RMSE 评价结果 用 7 种潜在概率分布与日降水量序列进行拟合，以 RMSE 为拟合优度的评价

指标，各分布的 RMSE 如图 3 所示。KAP、P-Ⅲ和 G2 相比于其它分布优势明显，这三种分布的 RMSE
和分位数如图 4 所示。绘制 KAP 和 P-Ⅲ分布、P-Ⅲ和 G2 分布的 RMSE 散点图，重点考查这三种分布

— 1252 —