Page 110 - 2022年第53卷第5期

（3）结合先验分布和现场试验数据，根据贝叶
斯公式求得后验分布 g（θ|x），为求解方便采用混合
Gibbs抽样的方法对后验分布进行模拟仿真求解；
（4）通过后验分布的特征值确定在一定可靠度
条件下各级配参数的估计值，此外根据贝叶斯方
法更新后的威布尔分布作为总体分布，产生随机
数作为压实质量评估模型中坝料级配特征参数的
输入指标。
2.1 贝叶斯理论 贝叶斯理论充分利用了先验信息
和现场试验信息，通过现场试验信息对先验信息进
行修正得到更为准确的后验信息。贝叶斯公式一般
表示为：

) f ( | x θ )g( ) θ
g( | θ x = （1）
∫ f ( | x θ )g( ) θ dθ
θ
式中：θ 为总体分布中的未知参数，即所要估计的
威布尔分布中的形状参数ξ和尺度参数 η；g（θ）为参
n
)
数θ的先验分布密度函数； f ( | x θ = ∏ f( ) |θ 为给定
x i
i = 1
θ 时 x 的条件概率分布，常称为似然分布；g（θ|x）为
i
给定 x 时 θ 的条件分布即后验分布； ∫ f ( | x θ )g( ) θ dθ
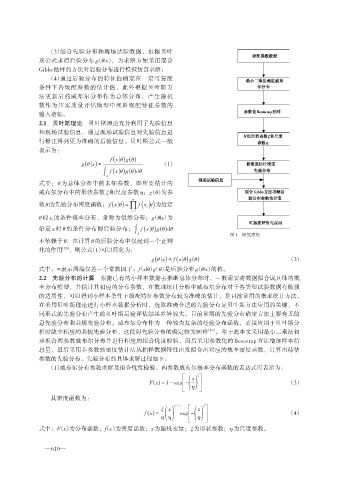
θ 图1 研究框架
不依赖于 θ，在计算 θ的后验分布中仅起到一个正则
化的作用 ［20］ ，则公式（1）可以简化为：
)
g( | θ x ∝ f ( | x θ )g( ) θ （2）
式中：∝表示两端仅差一个常数因子；f（x|θ）g（θ）是后验分布g（θ|x）的核。
2.2 先验分布的计算 根据已有的小样本数据去推断总体分布时，一般需要将数据拟合成具体的概
率分布模型，并估计其相应的分布参数，在数理统计分析中威布尔分布对于各类型试验数据有极强
的适用性，可以得到小样本条件下级配特征参数分布较为准确的估计，是目前常用的概率统计方法。
在采用贝叶斯理论进行小样本数据分析时，选取准确合适的先验分布是贝叶斯方法应用的关键，不
同形式的先验分布产生的贝叶斯后验评估结果差异较大。目前常用的先验分布确定方法主要有无信
息先验分布和共轭先验分布。威布尔分布作为一种较为复杂的经验分布函数，直接应用于贝叶斯分
析时缺少相应的共轭先验分布，这使得先验分布的确定较为困难 ［10］ 。鉴于此本文采用最小二乘法初
步拟合两参数威布尔分布并进行相应的拟合优度检验，而后采用参数化的 Bootstrap 方法增加样本信
息量，最后采用非参数核密度估计法从抽样数据特性出发拟合出对应的概率密度函数，计算出待估
参数的先验分布。先验分布的具体求解过程如下：
（1）威布尔分布参数求解及拟合优度检验。两参数威布尔概率分布函数的表达式可表示为：
ê ( ) ξ ù
é
x
F( ) x = 1 - expê- η ú ú （3）
ë û
其密度函数为：
( )
é
x
ξ x ξ - 1 ê ( ) ξ ù
f ( ) x = expê- ú ú （4）
η η ë η û
式中：F（x）为分布函数；f（x）为密度函数；x为随机变量；ξ为形状参数；η为尺度参数。

—610 —