Page 113 - 2022年第53卷第5期

5 2.5% 2.7 2.5%
50% 50%
97.5%
97.5%
4 2.4
形状参数ξ估值 3 尺度参数η估值 2.1

2 1.8

1 1.5
10000 20000 30000 10000 20000 30000
迭代次数 迭代次数
（a）形状参数 （b）尺度参数
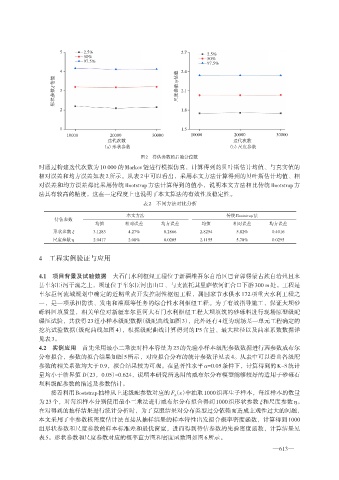
图2 待估参数的后验分位数
时通过构建迭代次数为 10 000 的 Markov 链进行模拟仿真，计算得到的贝叶斯估计均值、与真实值的
相对误差和均方误差如表 2所示。从表 2中可以看出，采用本文方法计算得到的贝叶斯估计均值、相
对误差和均方误差都比采用传统 Bootstrap 方法计算得到的值小，说明本文方法相比传统 Bootstrap 方
法具有较高的精度，这在一定程度上也说明了本文算法的有效性及稳定性。
表2 不同方法对比分析

本文方法 传统Bootstrap法
待估参数
均值 相对误差 均方误差 均值 相对误差 均方误差
形状参数ξ 3.1283 4.27% 0.2866 2.8254 5.82% 0.4016
尺度参数η 2.0417 2.08% 0.0205 2.1155 5.78% 0.0295

4 工程实例验证与应用

4.1 项目背景及试验数据 大石门水利枢纽工程位于新疆维吾尔自治区巴音郭楞蒙古族自治州且末
县车尔臣河干流之上，坝址位于车尔臣河出山口、与支流托其里萨依河汇合口下游300 m处。工程是
车尔臣河流域规划中确定的近期重点开发控制性枢纽工程，属国家节水供水 172 项重大水利工程之
一，是一项承担防洪、发电和灌溉等任务的综合性水利枢纽工程。为了有效指导施工，保证大坝砂
砾料回填质量，相关单位对新疆车尔臣河大石门水利枢纽工程大坝填筑的砂砾料进行现场原型级配
碾压试验，共获得 23组小样本级配数据（级配曲线如图 3），此外还有 4组为现场某一单元工程确定的
挖坑试验数据（级配曲线如图 4），根据级配曲线计算得到的 P5 含量、最大粒径以及曲率系数数据详
见表3。
4.2 实例应用 首先采用最小二乘法对样本容量为 23的先验小样本级配参数数据进行两参数威布尔

分布拟合，参数的拟合结果如图 5所示，对应拟合分布的统计参数详见表 4。从表中可以看出各级配
参数的相关系数均大于 0.9，拟合结果较为可观。在显著性水平 α=0.05条件下，计算得到的 K-S统计
量均小于临界值 D（23，0.05）=0.624，说明本研究所选用的威布尔分布模型能够较好的适用于砂砾石
坝料级配参数的描述及参数估计。
接着利用Bootstrap抽样从上述级配参数对应的F（x）中抽取1000组再生子样本，每组样本的数量
n
为 23个，对每组样本分别使用最小二乘法进行威布尔分布拟合得到 1000组形状参数 ξ和尺度参数 η。
在对得到的抽样结果进行统计分析时，为了克服结果对分布类型过分依赖而造成主观性过大的问题，

本文采用了非参数核密度估计法直接从抽样结果的样本特性出发拟合概率密度函数，计算得到 1000
组形状参数和尺度参数的样本标准差和最优窗宽，进而得到待估参数的先验密度函数，计算结果见
表5。形状参数和尺度参数对应的概率直方图和密度函数图如图6所示。

—613 —