Page 116 - 2022年第53卷第5期
P. 116
0.12
1.0
0.10
0.8
) 0.08 )
f h(ξ f h(η
0.06 0.6
0.4
0.04
0.02 0.2
0.00 0.0
0 5 10 15 20 25 30 30.0 30.5 31.0 31.5 32.0 32.5 33.0 33.5
形状参数ξ 尺度参数η
(a)P5含量
0.30 0.07
0.25 0.06
0.05
0.20
) )
f h(ξ f h(η 0.04
0.15
0.03
0.10
0.02
0.05
0.01
0.00
0.00
2 4 6 8 10 12 14 255 260 265 270 275 280 285 290 295
形状参数ξ 尺度参数η
(b)最大粒径
2.0
0.5
1.5
0.4
) )
f h(ξ 0.3 f h(η 1.0
0.2
0.5
0.1
0.0 0.0
1 2 3 4 5 6 7 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0
形状参数ξ 尺度参数η
(c)曲率系数
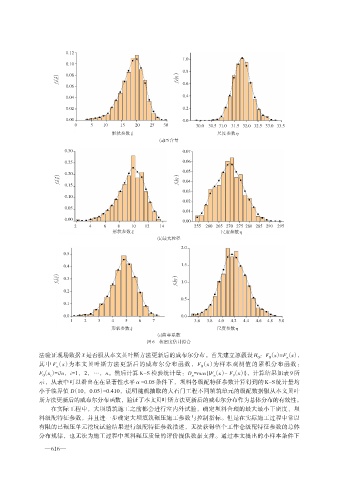
图6 核密度估计拟合
法验证现场数据X是否服从本文贝叶斯方法更新后的威布尔分布。首先建立原假设H :F(x)=F(x),
0 0 n
其中 F(x)为本文贝叶斯方法更新后的威布尔分布函数,F(x)为样本观测值的累积分布函数:
n
0
F(x)=i/n,i=1,2,…,n。然后计算 K-S 检验统计量:D =max{|F(x)- F(x)},计算结果如表 9 所
|
n
i
n
0
0
示,从表中可以看出在在显著性水平 α =0.05条件下,坝料各级配特征参数计算得到的 K-S统计量均
小于临界值 D(10,0.05)=0.410,说明随机抽取的大石门工程不同填筑单元的级配数据服从本文贝叶
斯方法更新后的威布尔分布函数,验证了本文贝叶斯方法更新后的威布尔分布作为总体分布的有效性。
在实际工程中,大坝填筑施工之前都会进行室内外试验,确定坝料合理的最大最小干密度、坝
料级配特征参数,并且进一步确定大坝填筑碾压施工参数与控制指标。但是在实际施工过程中常以
有限的已碾压单元挖坑试验结果进行级配特征参数描述,无法获得整个工作仓级配特征参数的总体
分布规律,也无法为施工过程中坝料碾压质量的评价提供数据支撑。通过本文提出的小样本条件下
—616 —