Page 115 - 2022年第53卷第5期

表4 拟合分布的统计参数
P5含量 最大粒径 曲率系数
ê ( ) 17.8562 ù ê( x 9.1520 ú ) ù ê ( x 4.5396 ú ) ù
é
é
é
x
( )
( )
( )
分布函数F n x F n x = 1 - expê- ú ú F n (x)= 1 - expê - ú F n x = 1 - expê- ú
ë 31.88 û ë 270.8184 û ë 4.2182 û
形状参数ξ 17.8562 9.1520 4.5396
尺度参数η 31.8800 270.8184 4.2182
相关系数 0.938 0.954 0.991
K-S统计量 0.1360 0.1965 0.0759
D(23，0.05) 0.624 0.624 0.624
表5 核密度估计参数及密度函数
形状参数ξ 尺度参数η
样本标准差σ ξ 最优窗宽h ξ 样本标准差σ η 最优窗宽h η
P5含量 3.8736 1.0314 0.3982 0.1060
最大粒径 1.8315 0.4876 6.6950 1.7826
曲率系数 0.9161 0.2439 0.2194 0.0584
n ( ) n ( )
( ) 1 ∑ K ξ - ξ i 1 ∑ K η - η i
密度函数 f h ξ = f h ( ) η =
1000h ξ i = 1 h ξ 1000h η i = 1 h η

经验值
经验值 1.0 经验值
1.0 拟合值 拟合值 1.0 拟合值
（x） 0.8 （x） 0.8 （x） 0.8
分布函数F 0.6 分布函数F 0.6 分布函数F 0.6
0.4
0.4
0.4
0.2
0.2
0.0 0.2
0.0 0.0
0 5 10 15 20 25
0 5 10 15 20 25 0 5 10 15 20 25
变量数 变量数 变量数
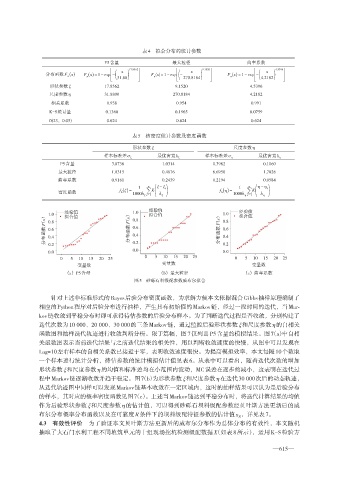
（a） P5含量 （b） 最大粒径 （c） 曲率系数
图5 砂砾石料级配参数威布尔拟合

针对上述非标准形式的Bayes后验分布密度函数，为求解方便本文依据混合Gibbs抽样原理编制了
相应的Python程序对后验分布进行抽样，产生具有初始值的Markov链，经过一段时间的迭代，当Mar⁃
kov链收敛到平稳分布时即可求得待估参数的后验分布样本。为了判断迭代过程是否收敛，分别构建了
迭代次数为10 000、20 000、30 000的三条Markov链，通过监控后验形状参数ξ和尺度参数η的自相关
函数图和抽样迭代轨迹进行收敛判断分析。限于篇幅，图7仅列出P5含量的模拟结果。图7（a）中自相
关函数图表示当前迭代结果与之前迭代结果的相关性，用以判断收敛速度的快慢，从图中可以发现在
Lag=10左右样本的自相关系数已接近于零，表明收敛速度很快。为提高模拟效率，本文每隔10个数取
一个样本进行统计分析，待估参数的统计模拟估计值见表 6。从表中可以看出，随着迭代次数的增加
形状参数ξ和尺度参数η的均值和标准差均在小范围内波动，MC误差在逐步的减小，这表明在迭代过
程中Markov链逐渐收敛并趋于稳定。图7（b）为形状参数ξ和尺度参数η在迭代30 000次后的动态轨迹，
从迭代轨迹图中同样可以发现Markov链基本收敛在一定区域内，这时的抽样结果可以认为是后验分布
的样本，其对应的概率密度函数见图7（c）。上述当Markov链达到平稳分布时，将迭代计算结果的均值
作为后验形状参数ξ和尺度参数 η的估计值，可以得到砂砾石坝料级配参数经贝叶斯方法更新后的威
布尔分布概率分布函数以及在可靠度R条件下的坝料级配特征参数的估计值x ，详见表7。
R
4.3 有效性评价 为了验证本文贝叶斯方法更新后的威布尔分布作为总体分布的有效性，本文随机
抽取了大石门水利工程不同填筑单元的十组现场挖坑检测级配数据 X（如表 8所示），运用 K-S检验方

—615 —