Page 118 - 2022年第53卷第5期

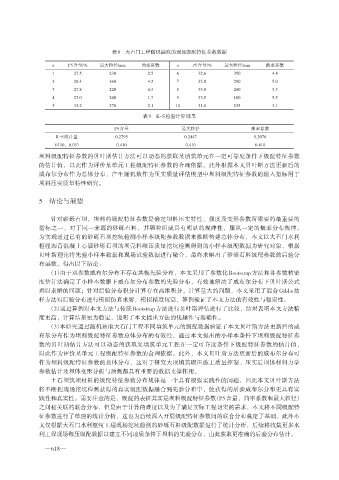
表8 大石门工程随机抽取的现场级配特征参数数据

n P5含量/% 最大粒径/mm 曲率系数 n P5含量/% 最大粒径/mm 曲率系数
1 27.5 230 2.5 6 32.6 350 4.4
2 28.4 360 4.2 7 32.0 280 5.0
3 27.8 220 4.3 8 33.0 240 3.5
4 27.0 240 1.7 9 33.5 180 5.5
5 33.2 270 2.1 10 31.8 235 3.1
表9 K-S检验计算结果

P5含量 最大粒径 曲率系数
K-S统计量 0.2795 0.2447 0.2076
D（10，0.05） 0.410 0.410 0.410

坝料级配特征参数的贝叶斯估计方法可以动态的获取某填筑单元在一定可靠度条件下级配特征参数
的估计值，以此作为评价某单元工程级配特征参数的合理依据。此外根据本文贝叶斯方法更新后的
威布尔分布作为总体分布，产生随机数作为压实质量评估模型中坝料级配特征参数的输入指标用于
坝料压实质量特性研究。

5 结论与展望

针对砂砾石坝，坝料的级配特征参数是确定坝料压实特性、强度及变形参数所需要的最重要的
指标之一，对于同一来源的砂砾石料，其颗粒组成具有明显的规律性，服从一定的概率分布规律。
为实现通过已有的砂砾石坝挖坑检测小样本级配参数数据来推断构建总体分布，本文以大石门水利
枢纽沥青混凝土心墙砂砾石坝的坝壳料碾压质量挖坑检测得到的小样本级配数据为研究对象，根据
贝叶斯理论将先验小样本数据和现场试验数据进行融合，最终求解出了砂砾石料级配参数的后验分
布函数。得出以下结论：
（1）由于双参数威布尔分布不存在共轭先验分布，本文采用了参数化 Bootstrap 方法和非参数核密
度估计法确定了小样本数据下威布尔分布参数的先验分布，有效地解决了威布尔分布下贝叶斯公式
难以求解的问题；针对后验分布积分计算存在高维积分，计算量大的问题，本文采用了混合 Gibbs抽
样方法对后验分布进行模拟仿真求解，模拟精度较高，算例验证了本文方法的有效性与稳定性。
（2）通过算例对本文方法与传统 Bootstrap 方法进行贝叶斯评估进行了比较，结果表明本文方法精
度更高，计算结果更为稳定，说明了本文提出方法的优越性与准确性。
（3）本研究通过随机抽取大石门工程不同填筑单元的级配数据验证了本文贝叶斯方法更新后的威
布尔分布作为坝料级配特征参数总体分布的有效性，通过本文提出的小样本条件下坝料级配特征参
数的贝叶斯估计方法可以动态的获取某填筑单元工程在一定可靠度条件下级配特征参数的估计值，
以此作为评价某单元工程级配特征参数的合理依据。此外，本文贝叶斯方法更新后的威布尔分布可
作为坝料级配特征参数的总体分布，这对于研究大坝填筑碾压施工质量控制、压实后坝体材料力学
参数估计及坝体变形分析与预测都具有重要的数据支撑作用。
土石坝筑坝材料的级配特征参数分布规律是一个具有很强实践性的问题，因此本文贝叶斯方法
将不断把现场挖坑检测获得的真实级配数据融合到先验分布中，使获得的后验威布尔分布更具有实
践性和真实性。需要注意的是，级配的表征其实是坝料级配特征参数（P5含量，曲率系数和最大粒径）
之间相关联的联合分布，但是由于计算的难度以及为了满足实际工程切实的需求，本文将不同级配特
征参数进行了单独的统计分析，这也为后续深入开展级配特征参数间的联合分布奠定了基础。此外本
文仅根据大石门水利枢纽工程现场挖坑检测的砂砾石料级配数据进行了统计分析，后续将收集更多水
利工程现场碾压级配数据以建立不同地质条件下坝料的先验分布，由此获取更准确的后验分布估计。

—618 —