Page 66 - 2022年第53卷第11期

式（１８）代入式（８）得
ｂ Δ ｙ ＋ ｃ Δ Ｑ ＝ Ｄ （１９）
３，０ ３，０ ３，０ ３，０ ３，０
ｅＦ ｅＫ
ｓ ４，Ｑ ３，０ ｓ ２
式中：ｂ ＝ ｅ；ｃ ＝ ａ－ ；Ｄ ＝－ － Ｆ 。
３，０ ３ ３，０ ３ ３，０ ３０
Ｋ Ｋ
１ １
对整个输水系统进行数值求解时，某一迭代步的计算程序为：
（ １）利用双扫法的消元过程计算渠道 １和渠道 ２的矩阵 Ｂ和列向量 Ｐ的 元素 Ｕ 、Ｗ 、Ｐ 、
１，ｉ
１，ｉ
１，ｉ
Ｕ 、Ｗ 和 Ｐ （ｉ ＝ ０ ，１，…，２ｍ，ｊ ＝ ０ ，１，…，２ｎ）；
２，ｊ
２，ｊ
２，ｊ
（ ２）利用式（１９）确定渠道 ３进口边界的双扫法系数，ｂ 、ｃ 和 Ｄ ；
３，０ ３，０ ３，０
（ ３）用双扫法的回代过程求解渠道 ３各计算节点的水位增量和流量增量；
（ ４）利用式（１８）、（１７）、（１６）、（１５）和（１４）依次求解 Δ ｙ、Δ Ｑ 、Δ ｙ 、Δ Ｑ 和 Δ ｙ ；
１，ｍ
１，ｍ
２，ｎ
ｓ
２，ｎ
（５）利用双扫法的回代过程求解渠道 １和渠道 ２各计算节点的水位增量和流量增量。
当配水池具有 Ｍ个进水、Ｎ个出水时（Ｍ、Ｎ为任意正整数），控制方程包括 Ｍ个进水与配水池的
能量守恒、配水池与 Ｎ个出水的能量守恒以及水体的质量守恒方程，可参照式（１）—（５），方程数量
为 Ｍ＋ Ｎ ＋ １ 。求解方法与 “一进、两出、一溢” 配水枢纽类似，即，利用双扫法的消元过程计算 Ｍ个
进水和 Ｎ － １ 个出水末节点的水位增量与流量增量关系；结合推求的 Ｍ＋ Ｎ ＋ １ 个控制方程，求解第 Ｎ个
出水首节点的水位增量与流量增量关系；利用回代过程求解第 Ｎ个出水所有节点的水位增量与流量增
量；求解其他渠道所有节点的水位增量与流量增量。当某些进水或出水是有压流动时，可采用窄缝法
进行求解。即假设管道顶部有一条非常窄的缝隙，既不增加管道的截面积，也不增加水力半径，宽
度为 ［１７］
２
Ｂ ＝ ｇＡ?ａ （２０）
２
式中：Ｂ为缝隙宽度，ｍ；Ａ为有压流动的截面积，ｍ ；ａ为水击波速，ｍ?ｓ。
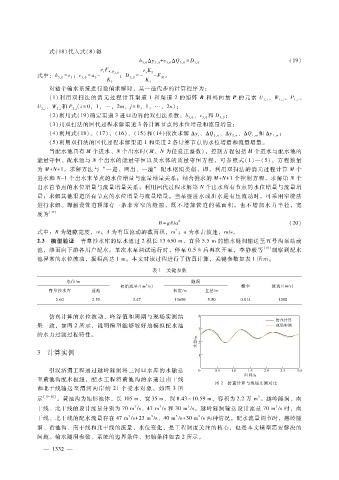
２．３ 模型验证 青草沙水库的原水通过 ２根长 １３６５０ｍ、直径 ５．５ｍ的输水隧洞输送至五号沟泵站前
池，继而向下游各用户配水。某次水泵调试运行时，停泵 ０．５ｈ后再次开泵，李静毅等 ［１８］ 观察到配水
池异常的水位波动，振幅高达 １ｍ。本文对该过程进行了仿真计算，关键参数如表 １所示。

表 １ 关键参数
水位?ｍ 隧洞
３
初始流量?（ｍ ?ｓ） 糙率 波速?（ｍ?ｓ）
青草沙水库 前池 长度?ｍ 直径?ｍ
２．６０ ２．５５ ３．４７ １３６５０ ５．５０ ０．０１４ １３００

仿真计算的水位波动、峰谷值和周期与现场实测结
果一致，如图 ２所示，说明模型能够较好地模拟配水池
的水力过渡过程特性。

３ 计算实例

引汉济渭工程通过越岭隧洞将三河口水库的水输送
至黄池沟配水枢纽，配水工程将黄池沟的水通过南干线
图 ２ 仿真计算与现场实测对比
和北干线输送至渭河两岸 的 ２１个受水对 象，如 图 ３所
３
示 ［１９ － ２０］ 。黄池沟为矩形池体，长 １０５ｍ、宽 ３５ｍ、深 ８．４３～１０．５９ｍ，容积为 ２．２万 ｍ 。越岭隧洞、南
３
３
３
３
干线、北干线的设计流量分别为 ７０ｍ ?ｓ、４７ｍ ?ｓ和 ３０ｍ ?ｓ。越岭隧洞输送设计流量 ７０ｍ ?ｓ时，南
３
３
３
３
干线、北干线的配水流量存在 ４７ｍ ?ｓ ＋ ２３ｍ ?ｓ、４０ｍ ?ｓ ＋ ３０ｍ ?ｓ两种情况。配水流量调节时，越岭隧
洞、黄池沟、南干线和北干线的流量、水位变化，是工程调度关注的核心，也是本文模型需要解决的
问题。输水隧洞参数、系统的边界条件、初始条件如表 ２所示。
３
— １ ３ ２ —