Page 94 - 2023年第54卷第1期

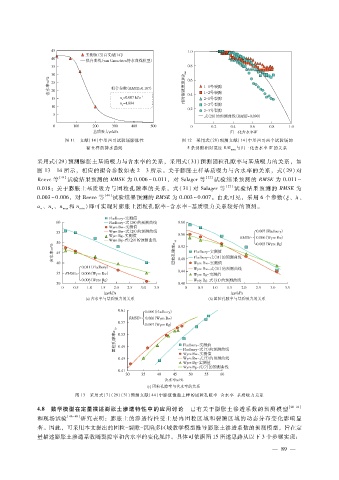
图 １１ 文献［１４］中墨西哥试验场膨胀性 图 １２ 采用式（２８）预测文献［１４］中墨西哥两个试验场的
黏土样的持水曲线 ５条裂隙相对宽度 Ｂ?Ｂ ｍａｘ 与归一化含水率 Ｗ的关系

采用式（２９）预测膨胀土基质吸力与含水率的关系，采用式（３１）预测团粒孔隙率与基质吸力的关系，如
图 １３—１４所示，相应的拟合参数如表 ２—３所示。关于膨胀土样基质吸力与含水率的关系，式（２９）对
Ｒｅｅｖｅ等 ［４４］ 试验结果预测的 ＲＭＳＥ为 ０．００６～０．０１１，对 Ｓａｌａｇｅｒ等 ［２２］ 试验结果预测的 ＲＭＳＥ为 ０．０１１～
０．０１８；关于膨胀土基质吸力与团粒孔隙率的关系，式（３１）对 Ｓａｌａｇｅｒ等 ［２２］ 试验结果预测的 ＲＭＳＥ为
０．００３～０．００６，对 Ｒｅｅｖｅ等 ［４４］ 试验结果预测的 ＲＭＳＥ为 ０．００３～０．００７。由此可见，采用 ６个参数（ ξ 、λ 、
ａ、ｎ、ｎ 和 ｎ ）即可实现对膨胀土团粒孔隙率－ 含水率－ 基质吸力关系较好的预测。
ｖ
ｍａｘ
ｍｉｎ
ｖ

图 １３ 采用式（７）（２９）（３１）预测文献［４４］中膨胀性黏土样的团粒孔隙率－ 含水率－ 基质吸力关系

４．８ 数学模型在定量描述膨胀土渗透特性中的应用讨论 已有关于膨胀土渗透系数的预测模型 ［２０ － ２１］
和现场试验 ［４６ － ４８］ 研究表明：膨胀土的渗透特性受土层内团粒区域和裂隙区域的动态分布变化影响显
著。因此，可采用本文提出的团粒－ 裂隙－ 沉陷多区域数学模型推导膨胀土渗透系数的预测模型，旨在定
量描述膨胀土渗透系数随裂隙率和含水率的变化规律。具体可依据图 １５所述思路从以下 ３个步骤实现：

— ８ ９ —