Page 91 - 2023年第54卷第1期

面和试样盒四边设置刻度处进行拍照，记录裂隙和沉陷的形成和发展过程，进而在 ＭＡＴＬＡＢ软件中采
用图像二值化处理程序（图 ５），并结合 ＩｍａｇｅＪ软件及其像素比例尺分别计算试样的裂隙率和沉陷率。
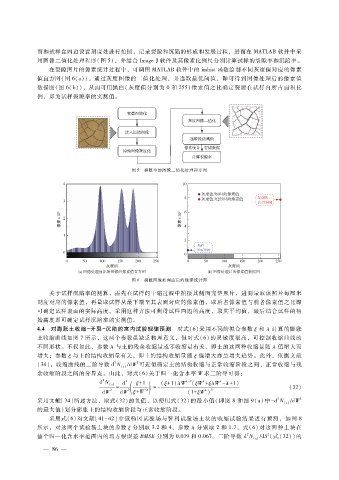
在裂隙图片的像素统计过程中，可调用 ＭＡＴＬＡＢ软件中的 ｉｍｈｉｓｔ函数绘制不同灰度值对应的像素
值直方图（图 ６（ａ））。通过灰度图像的二值化处理，并选取最优阈值，即可得到图像处理后的像素值
数据图（图 ６（ｂ）），从而可用黑白（灰度值分别为 ０和 ２５５）像素值之比确定裂隙在试样内所占面积比
例，即为试样裂隙率的实测值。

图 ５ 裂隙率的图像二值化处理程序图

图 ６ 裂隙图像处理前后的像素统计图

关于试样沉陷率的测算，需先在试样的干缩过程中拍摄其侧面完整照片，进而量取该照片每厘米
刻度对应的像素值，再量取试样从最下端至其表面对应的像素值，取后者像素值与前者像素值之比即
可确定试样表面的实际高度。采用这种方法可测得试样四边的高度，取其平均值，最后结合试样的初
始高度即可确定试样沉陷率的实测值。
４．４ 对膨胀土收缩－ 开裂－ 沉陷的室内试验规律预测 对式（６）采用不同的拟合参数 ξ 和 λ计算的膨胀
土收缩曲线如图 ７所示，这两个参数虽缺乏物理意义，但对式（６）的灵敏度很高，可控制收缩曲线的
不同形状。不仅如此，参数 λ与土的残余收缩量或零收缩量有关，即土的这两种收缩量随 λ值增大而
增大；参数 ξ 与土的结构收缩量有关，即土的结构收缩量随 ξ 值增大亦呈增大趋势。此外，依据文献
２
２
［３４］，收缩曲线的二阶导数 ｄＮ ?ｄＷ 可近似确定土的结构收缩与正常收缩阶段之间、正常收缩与残
（ａ）
余收缩阶段之间的分界点。由此，对式（ ６）关于归一化含水率 Ｗ求二阶导可得：
２
λ － ２
λ
ｄＮ ｄ ２ ξ ＋ １ （ ξ ＋ １ ） λ Ｗ （ ξ Ｗ ＋ ξλ Ｗ － λ ＋ １ ）
λ
（ａ） ２( － λ)
＝ ＝－ （３２）
λ
ｄＷ ２ ｄＷ ξ ＋ Ｗ （ １ ＋ ξ Ｗ ） ３
２
采用文献［ ３４］所述方法，取式（３２）的负值，以便用式（３２）的最小值（即图 ８和图 ９（ａ）中 － ｄＮ ?ｄＷ ２
（ａ）
的最大值）划分膨胀土的结构收缩阶段与正常收缩阶段。
采用式（ ６）对文献［４１ － ４２］中俄勒冈试验场与智利试验场土块的收缩试验结果进行预测，如图 ８
所示，对这两个试验场土块的参数 ξ 分别取 ３．２和 ４，参数 λ分别取 ２和 １．７，式（６）对这两种土块在
２
２
整个归一化含水率范围内的均方根误差 ＲＭＳＥ分别为 ０．０３９和 ０．０６７。二阶导数 ｄＮ ?ｄＳ（式（３２））的
（ａ）
— ８ ６ —