Page 93 - 2023年第54卷第1期

４．５ 由膨胀土样的收缩试验结果预测土层的现场裂隙体积 为验证本文提出的数学模型在描述膨胀土
［４３］
干燥失水过程不同孔隙区域变化规律的有效性，采用式（ ６）（１０）（１７）预测 Ｈａｌｌａｉｒｅ 对膨胀土样进行
的收缩试验结果，并对在现场土层的裂隙进行模拟。采用 ξ ＝ ４．５ 、λ ＝ ３．３ 、ｎ ＝ ０．５０４ 、ｎ ＝ ０．３０８ 、
ｍａｘ
ｍｉｎ
ｎ （ｓ）ｍａｘ ＝ ０．０４５ 以及 ｗ ＝ ３７．７％可得到预测曲线。对比膨胀土样的收缩试验表明：式（６）对 Ｎ 的预测
ｍａｘ
（ａ）
结果较其实测值的均方根误差 ＲＭＳＥ为 ０．０２４；式 （１０）对 Ｎ 的预测结果较其实测值的均方根误差
（ｓ）
ＲＭＳＥ为 ０．０３０；式（１７）对 Ｎ 的预测结果较其实测值的均方根误差 ＲＭＳＥ为 ０．０２０，如图 １０（ａ），由
（ｃ）
此可见，采用同一组参数可较为准确地模拟膨胀土样的收缩、开裂和沉陷。此外，采用同一组参数，
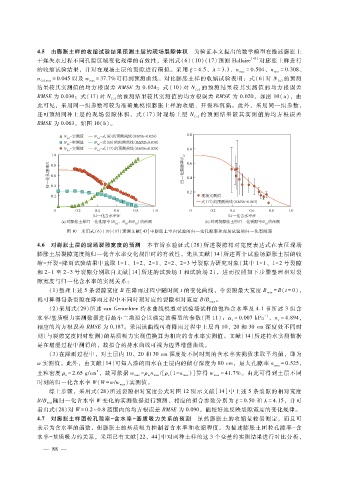
还可预测同种土层的 现场 裂隙 体积，式 （１７）对 现场土 层 Ｎ 的预 测结 果较 其实 测值 的均 方 根误差
（ｃ）
ＲＭＳＥ为 ０．０６３，如图 １０（ｂ）。

图 １０ 采用式（６）（１０）（１７）预测文献［４３］中膨胀土室内试验的归一化孔隙率和现场试验的归一化裂隙率

４．６ 对膨胀土层的现场裂隙宽度的预测 本节旨在验证式（２８）所述裂隙相对宽度表达式在表征现场
膨胀土层裂隙宽度随归一化含水率变化规律时的有效性。先从文献［ １４］所述两个试验场膨胀土层的收
缩－ 开裂－ 降雨试验结果中选取 １ － １、１ － ２、２ － １、２ － ２、２ － ３号裂隙为研究对象（其中 １ － １、１ － ２号裂隙
和 ２ － １至 ２ － ３号裂隙分别取自文献［１４］所述的试验场 １和试验场 ２），进而按照如下步骤整理相对裂
隙宽度与归一化含水率的实测关系：
（１）整理上述 ５条裂隙宽度 Ｂ在降雨过程中随时间 ｔ的变化曲线，令裂隙最大宽度 Ｂ ＝ Ｂ（ｔ ＝ ０ ），
ｍａｘ
则可算得每条裂隙在降雨过程中不同时刻对应的裂隙相对宽度 Ｂ?Ｂ 。
ｍａｘ
（ ２）采用式（２９）所述 ｖａｎＧｅｎｕｃｈｔｅｎ持水曲线模型对试验场试样的饱和含水率及 ４．１节所述 ３组含
－ １
＝ ０．００７ｋＰａ 、ｎ＝ ４．８９４，
ｖ
水率?基质吸力实测数据进行最小二乘拟合以确定该模型的参数（图 １１）：α ｖ
相应的均方根误差 ＲＭＳＥ为 ０．１８７。采用该曲线可将降雨过程中土层内 １０、２０和 ３０ｃｍ深度处不同时
刻（与裂隙宽度同时监测）的基质吸力实测值换算为相应的含水率实测值。文献［ １４］所述持水实测数据
是在增湿过程中测得的，故拟合的持水曲线可视为边界增湿曲线。
（３）在降雨过程中，对土层内 １０、２０和 ３０ｃｍ深度处不同时刻的含水率实测值求取平均值，即为
ｗ实测值。此外，由文献［１４］可知入渗的雨水在土层内的储存深度为 ８０ｃｍ，最大孔隙率 ｎ ＝ ０．５２５，
ｍａｘ
３
ｎ ?［ （１ － ｎ ）］算得 ｗ ＝ ４１．７％。由此可得到土层不同
土粒密度 ρ ｓ ＝ ２．６５ｇ?ｃｍ ，故可依据 ｗ ＝ ρ ｗ ｍａｘ ρ ｓ ｍａｘ ｍａｘ
ｍａｘ
时刻的归一化含水率 Ｗ（Ｗ＝ ｗ?ｗ ）实测值。
ｍａｘ
综上步骤，采用式（ ２８）所述裂隙相对宽度公式对图 １２所示文献［１４］中上述 ５条裂隙的相对宽度
Ｂ?Ｂ 随归一化含水率 Ｗ变化的实测数据进行预测，相应的拟合参数分别为 ξ ＝ ０．５０和 λ ＝ ４．１５ ，并可
ｍａｘ
看出式（ ２８）对 Ｗ＝ ０．２～０．８ 范围内的均方根误差 ＲＭＳＥ为 ０．０９０，能较好地反映裂隙宽度的变化规律。
４．７ 对膨胀土样团粒孔隙率－ 含水率 － 基质吸力关系的预测 虽然膨胀土的收缩量较易测定，而且可
表示为含水率的函数，但膨胀土的基质吸力控制着含水率和收缩程度。为描述膨胀土团粒孔隙率 － 含
水率－ 基质吸力的关系，采用已有文献［２２，４４］中对两种土样的这 ３个变量的实测结果进行对比分析，

— ８ ８ —