Page 95 - 2023年第54卷第1期
P. 95
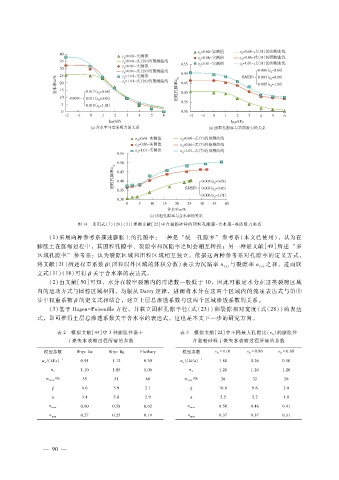
图 14 采用式(7)(29)(31)预测文献[22]中含黏粉砂样的团粒孔隙率- 含水率- 基质吸力关系
(1)采用两种参考系描述膨胀土的孔隙率:一种是 “统一孔隙率” 参考系(本文已使用),认为在
膨胀土在胀缩过程中,其团粒孔隙率、裂隙率和沉陷率之间会相互转换;另一种是文献[49]所述 “多
区域孔隙率” 参考系:认为裂隙区域和团粒区域相互独立。依据这两种参考系对孔隙率的定义方式,
将文献[21]所述权重系数 β (团粒以外区域的体积分数)表示为沉陷率 n 与裂隙率 n 之和,进而联
(s) (c)
立式(11)(18)可得 β 关于含水率的表达式。
( 2)由文献[50]可知,水分在较窄裂隙内的雷诺数一般低于 10,因此可假定水分在这类裂隙区域
内的运动方式与团粒区域相同,均服从 Darcy定律,进而将水分在这两个区域内的流速表达式与第①
步中权重系数 β 的定义式相结合,建立土层总渗透系数与这两个区域渗透系数的关系。
( 3)基于 Hagen - Poiseuille方程,并联立团粒孔隙半径(式(23))和裂隙相对宽度(式(28))的表达
式,即可推得土层总渗透系数关于含水率的表达式。这也是本文下一步的研究方向。
表 2 模拟文献[44]中 3种膨胀性黏土 表 3 模拟文献[22]中不同最大孔隙比(e)的膨胀性
0
干燥失水收缩过程所需的参数 含黏粉砂样干燥失水收缩过程所需的参数
=
=
=
模型参数 WryeBw WryeBg Fladbury 模型参数 e 0 1.01 e 0 0.86 e 0 0.68
α v ?(kPa) - 1 0.91 1.12 0.30 α v ?(kPa) - 1 1.80 0.26 0.10
1.10 1.05 1.06 1.20 1.20 1.20
n v n v
w max ?% 55 51 60 w max ?% 38 32 26
ξ 4.6 3.9 2.1 ξ 16.0 9.6 2.0
λ 3.4 3.8 2.9 λ 2.5 2.2 1.8
0.60 0.58 0.62 0.50 0.46 0.41
n max n max
0.27 0.25 0.19 0.37 0.37 0.31
n min n min
— 9 0 —