Page 44 - 2023年第54卷第3期

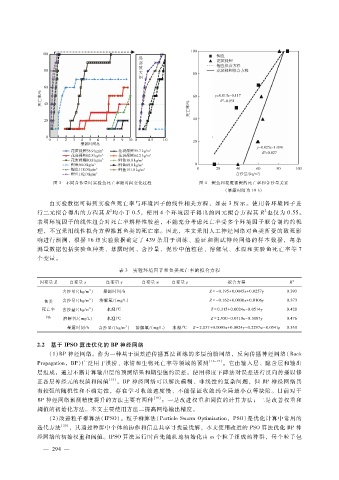
图 ３ 不同含沙量时实验鱼死亡率随时间变化过程 图 ４ 鲤鱼和花斑裸鲤的死亡率和含沙量关系
（暴露时间为 １０ｈ）

由实验数据可得到实验鱼死亡率与环境因子的线性相关方程，如表 ３所示。使用各环境因子进
２
２
行二元拟合得出的方程其 Ｒ均小于 ０．５，使用 ４个环境因子得出的四元拟合方程其 Ｒ 也仅为 ０．５５。
表明环境因子的线性组合对死亡率解释性较差，不能充分考虑死亡率受多个环境因子联合制约的机
理，不宜采用线性拟合方程推算鱼类的死亡率。因此，本文采用人工神经网络对鱼类所受的致死影
响进行预测，根据 １６组实验数据确定了 ４３９条用于 训练、验 证 和 测试 神 经 网络 的 样本 数 据，每条
测量数据包括实验鱼种类、暴露时间、含沙量、泥沙中值粒径、溶解氧、水温和实验鱼死亡率等 ７
个变量。

表 ３ 实验环境因子和鱼类死亡率的拟合方程

因变量 Ｚ 自变量 ｘ 自变量 ｙ 自变量 ｗ 自变量 ｐ 拟合方程 Ｒ ２
３
含沙量?（ｋｇ?ｍ ） 暴露时间?ｈ Ｚ ＝－ ０．１９５ ＋ ０．００４５ ｘ ＋ ０．０２５７ ｙ ０．３９３
３
鱼类 含沙量?（ｋｇ?ｍ ） 溶解氧?（ｍｇ?Ｌ） Ｚ ＝－ ０．１６２ ＋ ０．００３０ｘ ＋ ０．０１０６ｙ ０．３７３
３
死亡率 含沙量?（ｋｇ?ｍ ） 水温?℃ Ｚ ＝ ０．３１５ ＋ ０．００２４ｘ － ０．０５１４ｙ ０．４２０
?％ 溶解氧?（ｍｇ?Ｌ） 水温?℃ Ｚ ＝ ２．９５０ － ０．０７１０ｘ － ０．３０８７ｙ ０．４７６
３
暴露时间?ｈ 含沙量?（ｋｇ?ｍ ） 溶解氧?（ｍｇ?Ｌ） 水温?℃ Ｚ ＝ ２．０５７ ＋ ０．０００３ｘ ＋ ０．００２４ｙ － ０．２２９７ｗ － ０．０５４１ｐ ０．５５０

２．２ 基于 ＩＰＳＯ算法优化的 ＢＰ神经网络
（１）ＢＰ神经网络。作为一种基于误差逆传播算法训练的多层前馈网络，反向传播神经网络（Ｂａｃｋ
Ｐｒｏｐａｇａｔｉｏｎ ，ＢＰ）广泛用于洪涝、冰情和生物死亡率等领域的预测 ［１６ － １７］ 。它由输入层、隐含层和输出
层组成，通过不断计算输出层的预测结果和期望值的误差，使用梯度下降法对误差进行反向传播以修
正各层神经元的权值和阈值 ［１８］ 。ＢＰ神经网络可以解决模糊、非线性的复杂问题，但 ＢＰ神经网络具
有较强的随机性和不确定性，存在学习收敛速度慢、不能保证收敛到全局最小点等缺陷。目前对于
ＢＰ神经网络预测精度提升的方法主要有两种 ［１９］ ：一是改进权重和阈值的计算方法；二是改善权重和
阈值的初始化方法。本文主要使用方法二提高网络输出精度。
（ ２）改进粒子群算法（ＩＰＳＯ）。粒子群算法（ＰａｒｔｉｃｌｅＳｗａｒｍ Ｏｐｔｉｍｉｚａｔｉｏｎ，ＰＳＯ）是优化计算中常用的
迭代方法 ［２０］ ，其通过种群中个体的协作和信息共享寻找最优解，本文使用改进的 ＰＳＯ算法优化 ＢＰ神
经网络的初始权重和阈值。ＩＰＳＯ算法运行时首先随机地初始化由 ｍ个粒子组成的种群，每个粒子包

— ２ ９ —
４