Page 49 - 2023年第54卷第3期

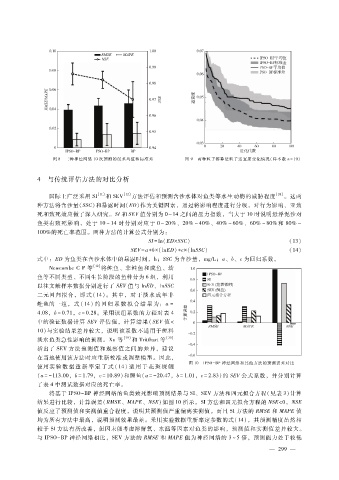
图 ８ 三种神经网络 １０次预测的误差均值和标准差 图 ９ 两种粒子群算法粒子适宜度变化情况（样本数 ｎ ＝ １０ ）

４ 与传统评估方法的对比分析

［１１］
国际上广泛采用 ＳＩ 和 ＳＥＶ ［１２］ 方法评估和预测含沙水体对鱼类等水生动物的威胁程度 ［２８］ 。这两
种方法将含沙量（ＳＳＣ）和暴露时间（ＥＤ）作为关键因素，通过将影响程度进行分级，对行为影响、亚致
死和致死效应做了深入研究。ＳＩ和 ＳＥＶ值分别为 ０～１４之间的压力指数，当大于 １０时说明悬浮泥沙对
鱼类有致死影响，处于 １０～１４时分别对应于 ０～２０％、２０％～４０％、４０％～６０％、６０％～８０％和 ８０％～
１００％的死亡率范围。两种方法的计算公式分别为：
ＳＩ ＝ ｌｎ （ＥＤ × ＳＳＣ） （１３）
ＳＥＶ ＝ ａ ＋ ｂ × （ｌｎＥＤ） ＋ ｃ × （ｌｎＳＳＣ） （１４）
式中：ＥＤ为鱼类在含沙水体中的暴露时间，ｈ；ＳＳＣ为含沙量，ｍｇ?Ｌ；ａ、ｂ、ｃ为回归系数。
ＮｅｗｃｏｍｂｅＣＰ等 ［１２］ 将鲑鱼、非鲑鱼和成鱼、幼
鱼等不同类型、不同生长阶段的鱼种分为 ６组，利用
以往文献样本数据分别进行了 ＳＥＶ值与 ｌｎＥＤ、ｌｎＳＳＣ
二元回归拟合，即式（１４）。其中，对于淡水成年非
鲑鱼的一 组，式 （１４）的 回 归 系 数 拟 合 结 果 为：ａ ＝
４．０８ ，ｂ ＝ ０．７１ ，ｃ ＝ ０．２８ 。采用该组系数的方程对表 ４
中的验证数据计算 ＳＥＶ评估值，计算结果（ＳＥＶ值 ＜
１０ ）与实验结果差异较大，说明该系数不适用于鲤科
淡水鱼类急性影响的预测。Ｘｕ等 ［２９］ 和 Ｔｒｉｔｔｈａｒｔ等 ［３０］
指出了 ＳＥＶ方法预测值和观察值之间的差异，建议
在当地使用该方法时应重新校准或调整模型。因此，
图 １０ ＩＰＳＯ － ＢＰ神经网络和其他方法的预测误差对比
使用实 验 数 据 重 新 率 定 了 式 （ １４）适 用 于 花 斑 裸 鲤
（ ａ ＝－ １１３．００，ｂ ＝ １．７９，ｃ ＝ １０．８９）和鲤鱼（ａ ＝－ ２０．４７，ｂ ＝ １．０１，ｃ ＝ ２．８３）的 ＳＥＶ公式系数，并分别计算
了表 ４中测试数据对应的死亡率。
将基于 ＩＰＳＯ － ＢＰ神经网络的鱼类致死影响预测结果与 ＳＩ、ＳＥＶ方法和四元拟合方程（见表 ３）计算
结果进行比较，计算误差（ＲＭＳＥ、ＭＡＰＥ、ＮＳＥ）如图 １０所示。ＳＩ方法和四元拟合方程的 ＮＳＥ＜０，ＮＳＥ
值反应了预测值和实测值重合程度，说明其预测值严重偏离实测值。而且 ＳＩ方法的 ＲＭＳＥ和 ＭＡＰＥ值
均为所有方法中最高，说明预测效果最差。采用实验数据重新率定参数的式（ １４），其预测精度虽然相
较于 ＳＩ方法有所改善，但因未能考虑溶解氧、水温等因素对鱼类的影响，预测值和实测值差异较大。
与 ＩＰＳＯ － ＢＰ神经网络相比，ＳＥＶ方法的 ＲＭＳＥ和 ＭＡＰＥ值为神经网络的 ３～５倍，预测能力处于较低

— ２ ９ ９ —