Page 47 - 2023年第54卷第3期

ｎ
∑ （ ＾ｙ － ｙ） ２
ｉ
ｉ
ｉ ＝１
ＮＳＥ ＝ １ － （１１）
ｎ
∑ （ ＾ｙ － 珋 ２
ｙ）
ｉ
ｉ
ｉ ＝１
式中： ＾ｙ 、ｙ分别为神经网络输出值和期望值，即鱼类死亡率的预测值和实测值； 珋 期望值的平均
ｙ为
ｉ ｉ ｉ
值，即鱼类死亡率实测值的平均值；ｉ为样本数据组数；ｎ为全部样本数据个数。
（ ２）ＢＰ神经网络结构。建立 ＢＰ神经网络的关键是拓扑网络的构造，包括网络层和结点数量的选
定。本文使用的 ＢＰ神经网络训练算法为 Ｂａｙｅｓ正则化算法，学习率为 ０．０１。网络结构包含输入层、
隐含层和输出层 ３层，输入层与隐含层间选用双曲线正切函数 Ｔａｎｓｉｇ作为传递函数，隐含层与输出层
间的选取线性函数 Ｐｕｒｅｌｉｎ作为传递函数。ＢＰ神经网络隐含层的神经元个数取值依据式（１２）初步确定
为 ９～１３个，通过由小到大改变神经元个数训练并检验其精度，计算表明当隐含层神经元个数为 １２时
精度最高，最终确定神经元数为：输入层 ６个、隐含层 １２个、输出层 １个。
ｐ ＝ ｍ ＋ ｎ ＋ Ａ （１２）
槡
式中：ｐ为隐含层神经元数量；ｍ为输入参数数量；ｎ为输出参数数量；Ａ为［１，１０］之间的常数。
（３）ＩＰＳＯ算法参数。粒子群方法中的粒子种群规模对系统的收敛速度、准确性和稳定性都有影
响。增加种群规模可以提高算法的搜索精度，但会减慢算法的收敛时间。王维博等 ［２５］ 根据实验法推荐
将粒子群的种群规模设置为 ２０～５０。利用粒子群算法优化 ＢＰ神经网络时，其最大迭代次数通常为 １００～
３００次 ［２３，２６］ 。本文选取 ＩＰＳＯ算法参数为：粒子种群规模 ３０、迭代次数 １００次。
３．２ ＩＰＳＯ－ ＢＰ神经网络训练结果 对于实验得出的 ４３９条测量数据，使用 ４１９条对 ＩＰＳＯ － ＢＰ神经网
络进行训练和验证，其中随机选取的训练集占 ８０％，验证集占 ２０％ ［２７］ 。使用 ２０条数据作为测试数据
（测试集不用于神经网络训练），测试数据集的变量值基本覆盖了实验测量的范围，具有较强的代表
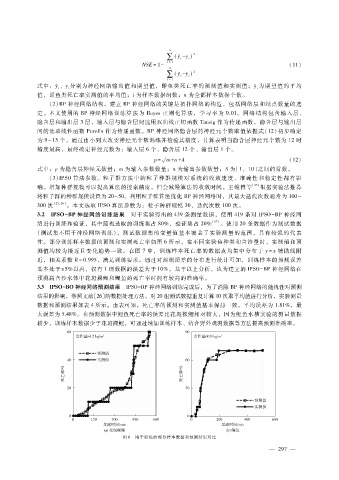
性。部分训练样本数据的预测和实测死亡率如图 ６所示，在不同实验鱼种类和含沙量时，实测值和预
测值均较为接近且变化趋势一致。在图 ７中，训练样本死亡率的数据点均集中分布于 ｙ ＝ ｘ辅助线附
近，相关系数 Ｒ ＝ ０．９９５，满足训练要求。通过对预测误差的分布进行统计可知，训练样本的预测误差
基本处于±５％以内，仅有 １组数据的误差大于 １０％。基于以上分析，认为建立的 ＩＰＳＯ － ＢＰ神经网络在
预测高含沙水体中花斑裸鲤和鲤鱼的死亡率时拥有较高的准确率。
３．３ ＩＰＳＯ － ＢＯ神经网络预测结果 ＩＰＳＯ － ＢＰ神经网络训练完成后，为了消除 ＢＰ神经网络的随机性对预测
结果的影响，参照文献［２６］的数据处理方法，对 ２０组测试数据重复计算 １０次取平均值进行分析，实验测量
数据和预测结果如表 ４所示。由表可知，死亡率的预测和实测值基本保持一致，平均误差为 １．８１％，最
大误差为 ５．４８％。在预测数据中鲤鱼死亡率的误差比花斑裸鲤相对较大，因为鲤鱼水槽实验的测量数据
较少，训练样本数据少于花斑裸鲤，可通过增加训练样本、结合野外观测数据等方法提高预测准确率。

图 ６ 用于训练的部分样本数据和预测结果对比

— ２ ９ ７ —