Page 57 - 2023年第54卷第3期

模拟区域的长为 ２．５ｍ，宽为 ２ｍ，计算域由 ３片不锈钢片组成，３块钢片的坡度均为 ０．０５。在计算域
内布置两面挡水墙来增加汇流难度，流域的布置及尺寸参见文献［ ３１］。区域的出口为右侧两面挡水墙
中间的位置。设计了两组降雨过程，第一组的降雨强度为 ５．２８ｍｍ?ｍｉｎ，降雨历时 ４５ｓ；第二组在前 ２５ｓ
的降雨强度 ５．３３ｍｍ?ｍｉｎ，当降雨停止 ７ｓ后，再施加降雨，强度为 ５．２８ｍｍ?ｍｉｎ，持续时间为 ２５ｓ。
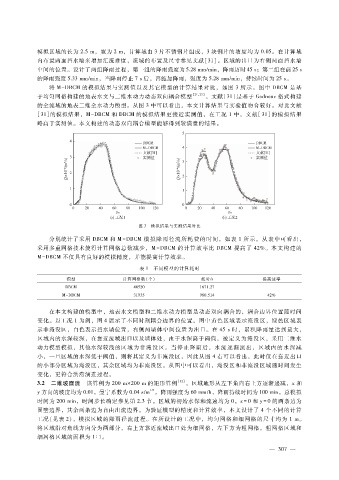
将 Ｍ－ ＤＢＣＭ的模拟结果与实测值以及其它模型的计算结果对比，如图 ３所示。图中 ＤＢＣＭ 是基
于均匀网格构建的地表水文与二维水动力动态双向耦合模型 ［２１，２５］ ，文献［３１］是基于 Ｇｏｄｎｏｕｖ格式构建
的全流域的地表二维全水动力模型。从图 ３中可以看出，本文计算结果与实验值吻合较好。对比文献
［ ３１］的模拟结果，Ｍ－ ＤＢＣＭ和 ＤＢＣＭ的模拟结果更接近实测值，在工况 １中，文献［３１］的模拟结果
略高于实测值。本文构建的动态双向耦合模型能够得到较满意的结果。

图 ３ 模拟结果与实测结果对比

分别统计了采用 ＤＢＣＭ和 Ｍ－ ＤＢＣＭ 模拟降雨径流所耗费的时间，如表 １所示。从表中可看出，
采用多重网格技术使得计算网格总数减少，Ｍ－ ＤＢＣＭ 的计算效率比 ＤＢＣＭ 提高了 ４２％。本文构建的
Ｍ－ ＤＢＣＭ不仅具有良好的模拟精度，并能提高计算效率。
表 １ 不同模型的计算耗时

模型 计算网格数（个） 耗时?ｓ 提高速率
ＤＢＣＭ ４８５２０ １６７１．２７
Ｍ－ ＤＢＣＭ ３１９３５ ９８０．５１４ ４２％

在本文构建的模型中，地表水文模型和二维水动力模型是动态双向耦合的，耦合边界位置随时间
变化。以工况 １为例，图 ４展示了不同时刻耦合边界的位置。图中黄色区域表示淹没区，绿色区域表
示非淹没区，白色表示挡水墙位置，右侧两墙体中间位置为出口。在 ４５ｓ时，累积降雨量达到最大，
区域内的水深较深，在靠近流域出口以及墙体处，由于水深高于阈值，被定义为淹没区，采用二维水
动力模型模拟，其他水深较浅的区域为非淹没区。当停止降雨后，水流逐渐流出，区域内的水深减
小，一旦区域的水深低于阈值，则将其定义为非淹没区，因此从图 ４右可以看出，此时仅在靠近出口
的小部分区域为淹没区，其余区域均为非淹没区。从图中可以看出，淹没区和非淹没区域随时间发生
变化，更符合洪涝演进过程。
３．２ 二维坡面流 该算例为 ２００ｍ × ２００ｍ的矩形算例 ［３２］ 。区域地形从左下角向右上方逐渐递减，ｘ和
１?３
ｙ方向的坡度均为 ０．０１。曼宁系数为 ０．０４ｓ?ｍ 。降雨强度为 ６０ｍｍ?ｈ，降雨持续时间为 １００ｍｉｎ。总模拟
时间为 ２００ｍｉｎ，时间步长确定参见第 ２．３节。区域的初始水深和流速均为 ０。ｘ ＝ ０ 和 ｙ ＝ ０ 的两条边为
固壁边界，其余两条边为自由出流边界。为验证模型的精度和计算效率，本文设计了 ４个不同的计算
工况（见表 ２），模拟区域的降雨径流过程。在所设计的工况中，均匀网格和细网格的尺寸均为 １ｍ。
将区域沿对角线方向分为两部分，右上方靠近流域出口处为细网格，左下方为粗网格，粗网格区域和
细网格区域的面积为 １∶１。

— ３ ０ ７ —