Page 115 - 2023年第54卷第4期

处，Ｘ和 Ｘ动力学结构一样，但 Ｘ发生了数值突变，此时 Ｑ ＝ ０，Ｒ＞０。当 ｕ值从 ３．５增加至 ３．７４时，
１ ２ ２
Ｌｏｇｉｓｔｉｃ时间序列将从四周期逐渐变为五周期状态，动力学结构也逐渐发生改变；在 ２１５—２８５处，Ｘ
１
和 Ｘ的动力学结构差异还不显著，对应的 Ｑ指数和 Ｒ指数均大于 ０，但处于很低的水平；在 ３１５—３８５
２
处，四周期序列 Ｘ与五周期序列 Ｘ的动力学结构明显不同，此时的 Ｑ指数和 Ｒ指数较 ２１５—２８５处也
２
１
较大。可以看出利用 Ｑ指数和 Ｒ指数可以有效地反映出系统间动力学结构差异和动力学距离。
３ 工程案例

３．１ 工程概况 本文以南水北调东线工程某泵站枢纽为例，该泵站枢纽由泵站、挡洪闸、进水闸、引
３
河等工程设施组成，主要功能为联合调水及区域排涝。泵站设计流量 １５０ｍ ?ｓ，调水期设计扬程 ６．０ｍ，
３
排涝期设计扬程 ６．６ｍ，安装立式全调节混流泵 ５台，单机设计流量 ３７．５ｍ ?ｓ，配套电机功率 ３５５０ｋＷ，
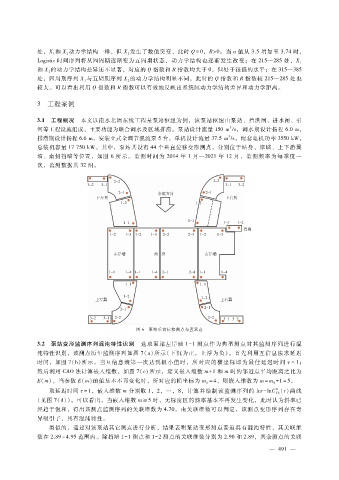
总装机容量 １７７５０ｋＷ。其中，泵站共设有 ４４个垂直位移变形测点，分别位于站身、岸墙、上下游翼
墙、南侧挡墙等位置，如图 ６所示。监测时间为 ２０１４年 １月—２０２１年 １２月，监测频率为每季度一
次，监测数据共 ３２组。

图 ６ 泵站垂直位移测点布置示意

３．２ 泵站变形监测序列混沌特性识别 选取泵站左岸墙 １ － １测点作为典型测点对其监测序列进行混
沌特性识别，该测点历年监测序列如图 ７（ａ）所示（下沉为正，上浮为负）。首先利用互信息法求延迟
时间，如图 ７（ｂ）所示，当互信息熵第一次达到极小值时，所对应的横坐标即为最佳延迟时间 τ ＝ １；
然后利用 ＣＡＯ法计算嵌入维数，如图 ７（ｃ）所示，定义嵌入维数 ｍ ＋ １和 ｍ时的邻近点平均距离之比为
Ｅ（ｍ），当参数 Ｅ（ｍ）的值基本不再变化时，所对应的横坐标为 ｍ ＝ ４，则嵌入维数为 ｍ＝ ｍ ＋ １ ＝ ５。
０
０
ｍ
取延迟时间 τ ＝ １ ，嵌入维数 ｍ分别取 １，２，…，８，计算并绘制该监测序列的 ｌｎｒ － ｌｎ Ｃ （ｒ）曲线
ＸＸ
（见图 ７（ｄ））。可以看出，当嵌入维数 ｍ ≥５时，无标度区的斜率基本不再发生变化，此时认为斜率已
经趋于饱和，得出该测点监测序列的关联维数为 ４．７０。由关联维数可以判定，该测点变形序列存在奇
异吸引子，具有混沌特性。
类似的，通过对该泵站其它测点进行分析，结果表明泵站变形测点普遍具有混沌特性，其关联维
数在 ２．８９～４．９５范围内。除挡墙 １ － １测点和 １ － ２测点的关联维数分别为 ２．９０和 ２．８９，其余测点的关联

— ４ ９ １ —