Page 9 - 2023年第54卷第7期

本研究收集整理了黄河流域水沙模拟研究在使用不同精度评价指标下的预测结果误差范围及可信度数
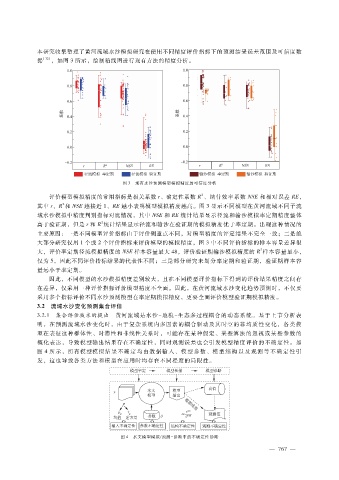
据 ［３２］ ，如图 ３所示，绘制箱线图进行现有方法的精度分析。

图 ３ 现有水沙预测模型模拟精度的可信度分析
２
评价模型模拟精度的常用指标是相关系数 ｒ、确定性系数 Ｒ、纳什效率系数 ＮＳＥ和相对误差 ＲＥ，
２
其中 ｒ、Ｒ和 ＮＳＥ越接近 １、ＲＥ越小表明模型模拟精度越高。图 ３显示不同模型在黄河流域不同子流
域水沙模拟中精度判别指标对比情况，其中 ＮＳＥ和 ＲＥ统计结果显示径流和输沙模拟率定期精度整体
２
高于验证期，但是 ｒ和 Ｒ统计结果显示径流和输沙在验证期的模拟精度优于率定期。出现这种情况的
主要原因：一是不同模型评价指标由于评价侧重点不同，对模型精度的评定结果不完全一致；二是绝
大部分研究仅用 １个或 ２个评价指标来评价模型的模拟精度，图 ３中不同评价指标的样本容量差异很
２
大，评价率定期径流模拟精度的 ＮＳＥ样本容量最大 ４８，评价验证期输沙模拟精度的 Ｒ样本容量最小，
仅为 ５，因此不同评价指标结果的代表性不同；三是部分研究未划分率定期和验证期，验证期样本容
量远小于率定期。
因此，不同模型的水沙模拟精度差别较大，且在不同模型评价指标下得到的评价结果精度之间存
在差异，仅采用一种评价指标评价模型精度不全面。因此，在黄河流域水沙变化趋势预测时，不仅要
采用多个指标评价不同水沙预测模型在率定期模拟精度，更要全面评价模型验证期模拟精度。
３．２ 流域水沙变化预测集合评估
３．２．１ 集合评估技术的提出 黄河流域是水沙 － 地貌 － 生态多过程耦合的动态系统。基于上节分析表
明，在预测流域水沙变化时，由于复杂系统内多因素的耦合驱动及其时空的非均质性变化，各类模
型在表征这种群体性、时滞性和非线性关系时，可能存在某种假定、某些算法的忽视或某些参数的
概化表达，导致模型输出结果存在不确定性，同时观测误差也会引发模型精度评价的不确定性。如
图 ４所示，所有模型模拟 结果 不确 定均由 数据输 入、模型 参 数、模 型 结 构 以 及 观 测 等 不 确 定 性 引
发，这也导致各类方法和模型在应用时均存在不同程度的局限性。

图 ４ 水文模型模拟?预测－ 诊断中的不确定性诊断

— ７ ６ ７ —