Page 7 - 2023年第54卷第8期

是第 ｉ个核函数；
式中：ｍ为核函数的数量，一般采用试错法来确定 ｍ，其范围一般为 １～５；函数 φ ｉ
ｗ
Ｙ为 ＭＤＮ对应权重参数的输出信息。
常用的核函数为高斯核函数，公式为：
１ （Ｘ － μ） ２
ｉ
（Ｙ Ｘ） ＝ － ２ （４）
φ ｉ ｅ ２ σ
ｉ
槡 ２ πσ ｉ
σ
式中：μ为期望值；σ为方差，采用指数函数处理，σ ＝ ｅｘｐ （Ｙ），以保证为非负值函数。
ＭＤＮ的输出变量 Ｙ元素个数为 ３ｍ。
ｆ
μ
μ
ｗ
ｗ
σ
Ｙ＝ ［Ｙ，…，Ｙ ，Ｙ ，…，Ｙ ，Ｙ σ ，…，Ｙ ］ （５）
ｍ ＋ １
２ｍ
３ｍ
２ｍ ＋ １
１
ｆ
ｍ

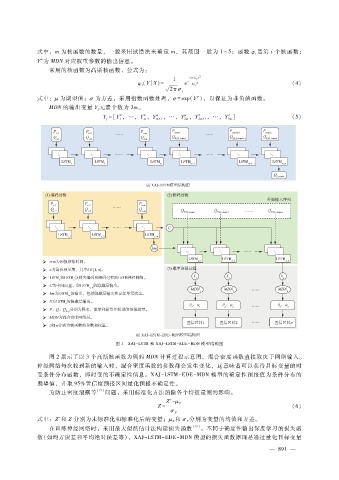
图 １ ＸＡＪ － ＬＳＴＭ和 ＸＡＪ － ＬＳＴＭ－ ＥＤＥ － ＭＤＮ模型结构图

图 ２展示了以 ３个高斯核函数为例的 ＭＤＮ计算过程示意图。混合密度函数直接取决于网络输入。
神经网络每次收到新的输入时，混合密度函数的参数都会发生变化，这意味着可以获得目标变量的时
变条件分布函数，即时变的不确定性信息。ＸＡＪ － ＬＳＴＭ－ ＥＤＥ － ＭＤＮ模型的确定性预报值为条件分布的
期望值，并取 ９５％置信度预报区间量化预报不确定性。
为防止密度泄露等 ［１９］ 问题，采用标准化方法消除各个特征量纲的影响。
Ｚ′ － μ Ｚ
Ｚ ＝ （６）
σ Ｚ
分别为变量的均值和方差。
式中：Ｚ′和 Ｚ分别为未标准化和标准化后的变量；μ Ｚ 和 σ Ｚ
在训练神经网络时，采用最大似然估计法构建损失函数 ［１９］ 。不同于确定性输出深度学习的损失函
数（如均方误差和平均绝对误差等），ＸＡＪ － ＬＳＴＭ－ ＥＤＥ － ＭＤＮ模型的损失函数原理是通过量化目标变量

— ８ ９ １ —