Page 126 - 2023年第54卷第9期

［Ｃ］ ＝ ａ［Ｍ］ ＋ ａ［Ｋ］ （１０）
０ １
ａ ａω ｎ
＝ ０ ＋ １ （１１）
ζ ｔ
２
２ ω ｎ
式中：［Ｃ］、［Ｍ］和［Ｋ］分别为阻尼矩阵、质量矩阵和刚度矩阵；ａ和 ａ分别为质量和刚度矩阵系数，
１
０
工程中一般忽略质量矩阵系数，即 ａ＝ ０ 。
０
假设结构振动是多阶模态的叠加，则质量矩阵和刚度矩阵可分别定义为多阶模态质量和模态刚度
构成的对角矩阵。若在水中进行结构动力学计算，则需在式（ １０）中考虑水体附加的质量矩阵、刚度矩
阵和阻尼矩阵。
第二步，通过调节数值阻尼，并基于数值计算得到不同的输出阻尼。
第三步，当输入阻尼与输出阻尼一致时，认为数值阻尼取值可靠。
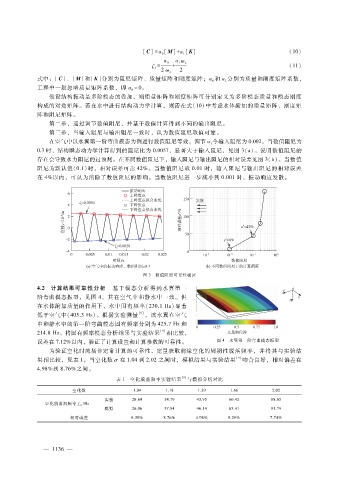
在空气中以水翼第一阶弯曲模态为例进行数值阻尼等效，调节 ａ令输入阻尼为 ０．００２。当数值阻尼为
１
０．３时，结构瞬态动力学计算得到的阻尼比为 ０．００５７，显著大于输入阻尼，见图 ３（ａ）。说明数值阻尼的
存在会导致水力阻尼的过预测。在不同数值阻尼下，输入阻尼与输出阻尼的相对误差见图 ３（ｂ）。当数值
阻尼为默认值（ ０．１）时，相对误差可达 ４２％。当数值阻尼取 ０．０１时，输入阻尼与输出阻尼的相对误差
在 ４％以内，可认为消除了数值阻尼的影响。当数值阻尼进一步减小到 ０．００１时，振动响应发散。

图 ３ 数值阻尼可靠性验证

４．２ 计算结果可靠性分析 基于模态分析得到水翼第一
阶弯曲模态振型，见图 ４，其在空气中和静水中一致。但
在水体附加质量的作用下，水中固有频率（ ２３０．１Ｈｚ）显著
低于空气中（ ４０５．３Ｈｚ）。根据实验测量 ［９］ ，该水翼在空气
中和静水中的第一阶弯曲模态固有频率分别为 ４２５．７Ｈｚ和
２１４．８Ｈｚ。将固有频率模态分析结果与实验结果 ［９］ 相比较，
误差在 ７．１２％以内，验证了计算设置和计算参数的可靠性。 图 ４ 水翼第一阶弯曲模态振型
为验证空化时流场非定常计算的可靠性，定量获取前缘空化的周期性脱落频率，并将其与实验结
果相比较，见表 １。当空化数 σ在 １．０４到 ２．０２之间时，模拟结果与实验结果 ［９］ 吻合良好，相对偏差在
４．９８％到 ８．７６％之间。
［９］
表 １ 空化脱落频率实验结果 与模拟分析对比
空化数 １．０４ １．１８ １．３９ １．６６ ２．０２
实验 ２８．６９ ３４．７９ ４３．９５ ６０．４２ ８８．６５
空化脱落涡频率 ｆ?Ｈｚ
ｃａ
模拟 ２６．８６ ３７．８４ ４６．１４ ６５．４１ ８１．７９
相对误差 ６．３８％ ８．７６％ ４．９８％ ８．２６％ ７．７４％

— １ １ ６ —
３