Page 127 - 2023年第54卷第9期
P. 127
5 结果与讨论
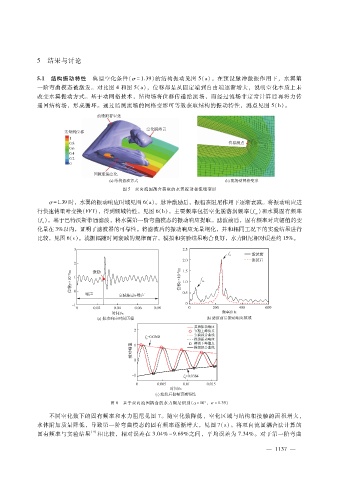
5.1 结构振动特性 典型空化条件( σ = 1.39 )的结构振动见图 5(a)。在预设脉冲激振作用下,水翼第
一阶弯曲模态被激发。对比图 4和图 5(a),位移都是从固定端到自由端逐渐增大,说明空化本质上未
改变水翼振动方式。基于动网格技术,结构场将位移传递给流场,而经过流场非定常计算后再将力传
递回结构场,形成循环。通过监测流场的网格变形可等效获取结构的振动特性,测点见图 5(b)。
图 5 双向流固耦合获取的水翼振动和流场变形
σ = 1.39 时,水翼的振动响应时域见图 6(a)。脉冲激励后,振幅在阻尼作用下逐渐衰减。将振动响应进
行快速傅里叶变换( FFT),得到频域特性,见图 6(b)。主要频率包括空化脱落涡频率(f)和水翼固有频率
ca
(f)。基于巴特沃斯带通滤波,将水翼第一阶弯曲模态的振动响应提取。滤波前后,固有频率对应幅值的变
n
化量在 3%以内,证明了滤波器的可靠性。将滤波后的振动响应无量纲化,并和相同工况下的实验结果进行
比较,见图 6(c)。就振幅随时间衰减的规律而言,模拟和实验结果吻合良好,水力阻尼相对误差约 15%。
图 6 基于双向流固耦合的水力阻尼识别( α = 10° ,σ = 1.39 )
不同空化数下的固有频率和水力阻尼见图 7。随空化数降低,空化区域与结构相接触的面积增大,
水体附加质量降低,导致第一阶弯曲模态的固有频率逐渐增大,见图 7(a)。将双向流固耦合法计算的
固有频率与实验结果 [9] 相比较,相对误差在 3.04%~9.69%之间,平均误差为 7.34%。对于第一阶弯曲
1
— 1 3 7 —