Page 96 - 2023年第54卷第9期

＝ ６０°）作用下坝体的响应进行研究。按照文献［２０］中的思路并拓展到三维场地，当垂直入射时在
α ＳＶ
底部输入入射波场，在四个侧面输入自由波场；当倾斜入射时在地基底面、右面和后面边界输入入射
波场，在前面和左面边界输入自由波场。
由于传统的波动输入方法推导依赖于几何传播模拟，几乎无法扩展到复杂场地的动力输入中，因
此采用文献［ ３４］中所提出的基于人工边界子模型的地震波输入方法，并将此扩展至三维空间。改进的
波动输入方法依据的基本原理是：只要能确定边界最外层节点的受力状态并输入，便能实现精确的外
源输入。因此将图 ８中地基模型最外层的边界进行单独的受力分析即可快速实现计算。此外，为反映
地质结构对地震波传播规律的影响，选取了均质地基作为对比，地基参数为表 ２中第一层的动力参
数。整套波场计算和节点力输入流程需要对 ＡＢＡＱＵＳ进行二次开发，不包括数据处理等过程，每组算
例的计算时间大约为 ２０ｈ（４８核计算）。

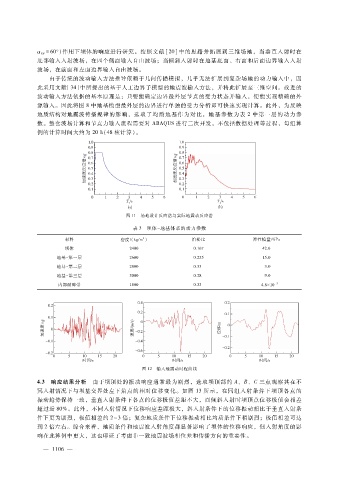
图 １１ 场地设计反应谱与实际地震动反应谱

表 ３ 坝体－ 地基体系的动力参数
３
材料 密度?（ｋｇ?ｍ ） 泊松比 弹性模量?ＧＰａ
坝体 ２４００ ０．１６７ ４２．６
地基－ 第一层 ２６００ ０．２３５ １５．０
地基－ 第二层 ２８００ ０．３５ ３．０
地基－ 第三层 ３０００ ０．２８ ９．０
内部破碎带 １８００ ０．３３ ４．８ × １０ － ５

图 １２ 输入地震动时程曲线

４．３ 响应结果分析 由于坝顶处的振动响应通常最为剧烈，选取坝顶部的 Ａ、Ｂ、Ｃ三点观察其在不
同入射情况下与坝基交界处左下角点的相对位移变化。如图 １３所示，在同组入射条件下坝顶各点的
振动趋势保持一致，垂直入射条件下各点的位移极值差距不大，而倾斜入射时坝顶点位移极值会相差
超过近 ８０％。此外，不同入射情况下位移响应差距极大，斜入射条件下的位移振动相比于垂直入射条
件下更为剧烈，极值相差约 ２～３倍；复杂地质条件下位移振动相比均质条件下稍剧烈；极值相差可达
到 ２倍左右。综合来看，地质条件和地震波入射角度都显著影响了坝体的位移响应，但入射角度的影
响在此算例中更大，这也印证了考虑非一致地震波场相位差和传播方向的重要性。

０
— １ １ ６ —