Page 92 - 2023年第54卷第9期

ＳＶ
{ Ｆ ＝ ｖ（ｘ，ｙ，ｔ）·（ ρ ｃｃｏｓ（２ θ ２ ） ＋ Ｃ ｃｏｓ θ ２ ） （６）
ＢＴ
Ｂｘ
Ｓ
ＳＶ
Ｓ
Ｂｙ
Ｆ ＝ ｖ（ｘ，ｙ，ｔ）·（ ρ ｃｓｉｎ（２ θ ２ ） ＋ Ｃ ｃｏｓ θ ２ ）
ＢＮ
分别为 Ｐ波和 ＳＶ波各自的入射角度；Ｃ 和 Ｃ 为应力型人工边界上法向和切向的黏性
式中：θ １ 和 θ ２
ＢＮ ＢＴ
系数；λ为场地的 Ｌａｍｅ常数；ｖ（ｘ，ｙ，ｔ）为输入的速度函数。
ＳＨ波的波场计算方式类似，只是由于波动为单向的出平面方向，所以式（２）中的位移矩阵等退
化为单独的数值，且需 变 换 相 应 的 单 元 刚 度 矩 阵 与 底 部 边 界 的 等 效 输 入 荷 载，其 显 式 表 达 Ｋ 和
ａｎｔｉ
ＳＨ
Ｆ 分别如下：
Ｂ
－ ２ ａ ＋ ２ － ２ ａ ＋ １ － ａ － １ ａ － ２
２
ρ ｃ － ２ ａ ＋ １ ２ ａ ＋ ２ ａ － ２ － ａ － １
Ｓ Ｈ
Ｋ ＝ × （７）
ａｎｔｉ
６ ａ － ａ － １ ａ － ２ ２ ａ ＋ ２ － ２ ａ ＋ １
槡
ａ － ２ － ａ － １ － ２ａ ＋ １ ２ａ ＋ ２
ＳＨ
Ｂ ＳＨ
Ｆ ＝ ２ ·ｖ（ｘ，ｙ，ｔ）·ρ ｃ ｃｏｓ θ ３ （８）
２
为 ＳＨ波的入射角度；ｃ 为出平面 ＳＨ波的波速；ａ ＝ （ Δ ｙ? Δ ｘ）。
式中：θ ３ ＳＨ
２．２ 上下行波分离 构成自由波场的入射波与反射波分别属于上行波和下行波；其中，上行波属于内
行波，这是在局部地形效应以及断层场地等复杂地震波场求解中需要单独计算的部分 ［２０］ 。以同组地震
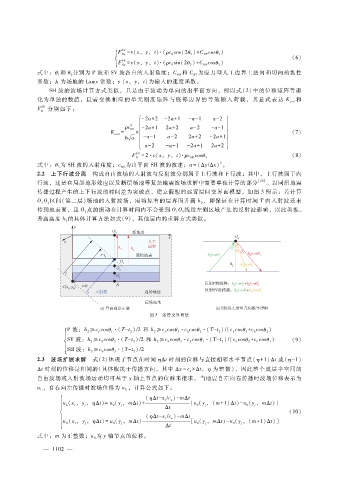
传播过程产生的上下行波的时间差为突破点，建立假想的远置层间交界面模型。如图 ３所示：若计算
ＯＯ区间（第二层）场地的入射波场，需将原有的层界面升高 ｈ，即保证在计算时间 Ｔ内入射波还未
１
２
２
传到地表面，且 Ｏ点的振动在计算时间内不会受到 ＯＯ线段左侧区域产生的反射波影响，以此类推。
４
２
１
升高高度 ｈ的具体计算方法如式（９），其他层内的求解方式类似。
２

图 ３ 远置交界面法

{ Ｐ波：ｈ≥ｃｃｏｓ θ １ ·（Ｔ － ｔ）?２和 ｈ≥ｃｃｏｓ θ １ ·ｃｃｏｓ θ ２ ·（Ｔ － ｔ）?（ｃｃｏｓ θ １ ＋ ｃｃｏｓ θ ２ ） ） （９）
Ｓ
２
２
Ｐ
２
Ｐ
Ｐ
２
Ｓ
Ｓ
Ｐ
２
·（Ｔ － ｔ）?（ｃｃｏｓ θ ２
·ｃｃｏｓ θ １
Ｐ
Ｓ
·（Ｔ － ｔ）?２和 ｈ≥ｃｃｏｓ θ ２
Ｓ
＋ ｃｃｏｓ θ １
２
ＳＶ波：ｈ≥ｃｃｏｓ θ ２
２
２
２ Ｓ ２
ＳＨ波：ｈ≥ｃｃｏｓ θ ３ ·（Ｔ － ｔ）?２
２．３ 波场扩展求解 式（２）体现了节点在时间 ηΔ ｔ时刻的位移与直接相邻水平节点（ η ＋ １ ） Δ ｔ或（ η － １ ）
Δ ｔ时刻的位移是相同的（具体取决于传播方向，其中 Δ ｘ ＝ ｃ× Δ ｔ，η为整数），因此整个成层半空间的
ｘ
自由波场或入射波场运动均可基于 ｙ轴上节点的位移来推求。当地震自左向右传播时波场位移表示为
ｕ，自右向左传播时波场位移为 ｕ，计算公式如下：
Ｒ
Ｌ
（ ηΔ ｔ － ｘ?ｃ） － ｍ Δ ｔ
ｉ ｘ
ｕ（ｘ，ｙ，ηΔ ｔ） ＝ｕ（ｙ，ｍ Δ ｔ） ＋ ［ｕ（ｙ，（ｍ ＋ １ ） Δ ｔ） － ｕ（ｙ，ｍ Δ ｔ）］
Ｌ ｉ ｊ ０ ｊ ０ ｊ ０ ｊ
Δ ｔ
（ １０）
（ ηΔ ｔ － ｘ?ｃ） － ｍ Δ ｔ
ｉ ｘ
ｕ（ｘ，ｙ，ηΔ ｔ） ＝ｕ（ｙ，ｍ Δ ｔ） － ［ｕ（ｙ，ｍ Δ ｔ） － ｕ（ｙ，（ｍ ＋ １） Δ ｔ）］
Ｒ ｉ ｊ ０ ｊ ０ ｊ ０ ｊ
Δ ｔ
式中：ｍ为正整数；ｕ为 ｙ轴节点的位移。
０
— １ １ ２ —
０