Page 94 - 2023年第54卷第9期
P. 94
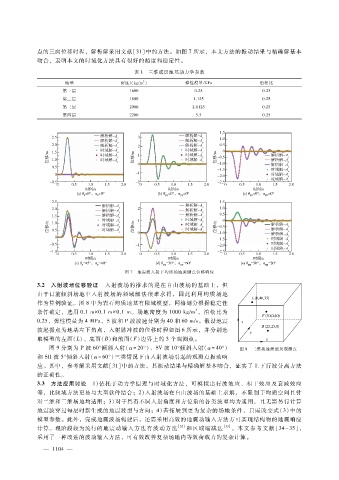
点的三向位移时程,解析解采用文献[31]中的方法。如图 7所示,本文方法的振动结果与精确解基本
吻合,表明本文的时域化方法具有很好的精度和稳定性。
表 1 三维成层地基动力学参数
3
地基 密度?(kg?m ) 弹性模量?GPa 泊松比
第一层 1600 0.25 0.25
第二层 1800 1.125 0.25
第三层 2000 2.8125 0.25
第四层 2200 5.5 0.25
图 7 地震波入射下均质场地关键点位移响应
3.2 入射波场位移验证 入射波场的推求的是在自由波场的基础上,但
由于目前倾斜场地中入射波场的频域解法很难求得,因此利用均质场地
作为算例验证。图 8中为岩石均质地基有限域模型,网格划分根据稳定性
3
条件确定,选用 0.1m × 0.1m × 0.1m。场地密度为 1000kg?m ,泊松比为
0.25,弹性模量为 4MPa,S波和 P波波速分别为 40和 60m?s。假设地震
波起振点为地基左下角点,入射脉冲波的位移时程如图 6所示,并分别选
取模型的左面( L)、底面(B)和前面(F)边界上的 3个观测点。
图 9分别为 P波 60°倾斜入射( α = 20°)、SV波 10°倾斜入射( α = 40°) 图 8 三维场地模型及观测点
和 SH波 5°倾斜入射( α = 60° )三类情况下由入射波场引起的观测点振动响
应。其中,参考解采用文献[ 31]中的方法。其振动结果与精确解基本吻合,证实了上下行波分离方法
的正确性。
3.3 方法应用讨论 1)依托于动力学原理与时域化方法,可模拟出行波效应、相干效应及衰减效应
等,比频域方法更易与大型软件结合;2)入射波场在自由波场的基础上求解,不限制于均质空间且针
对二维和三维场地均适用;3)对于具有不同入射角度和方位角的各类波型均为通用,且无需另行计算
地震波穿过每层时新生成的地震波型与方向;4)若拓展到更为复杂的场地条件,只需改变式(3)中的
模型参数。此外,完成地震波场构建后,还需采用高效的地震动输入方法方可实现结构物的地震响应
计算。现阶段较为流行的地震动输入方法有波动方法 [32] 和区域缩减法 [33] 。本文参考文献[34 - 35],
采用了一种改进的波动输入方法,可有效改善复杂场地内等效荷载力的复杂计算。
0
— 1 1 4 —