Page 106 - 2023年第54卷第10期

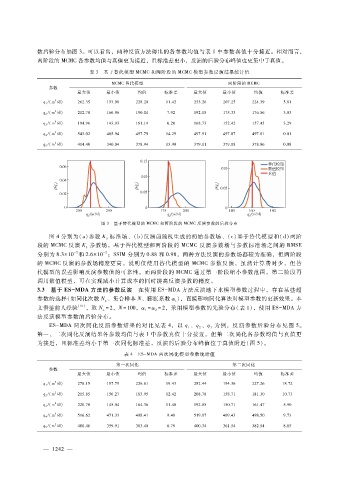
数后验分布如图 ３。可以看出，两种反演方法得出的各参数均值与表 １中参数真值十分接近。相对而言，
两阶段的 ＭＣＭＣ各参数均值与真值更为接近，且标准差更小，反演的后验分布峰值也更集中于真值。
表 ３ 基于替代模型 ＭＣＭＣ和两阶段的 ＭＣＭＣ模型参数反演结果统计值

ＭＣＭＣ替代模型 两阶段的 ＭＣＭＣ
参数
最大值 最小值 均值 标准差 最大值 最小值 均值 标准差
３
ｑ １ ?（ｍ ?ｄ） ２６２．３５ １９３．９８ ２２８．２０ １１．４２ ２３３．２６ ２０７．２５ ２２４．３９ ５．８１
３
ｑ ２ ?（ｍ ?ｄ） ２１２．７８ １６６．９６ １９０．０４ ７．９２ １９２．１５ １７５．３３ １７６．５６ ３．０３
３
ｑ ３ ?（ｍ ?ｄ） １８４．９６ １４３．９３ １６１．１９ ６．２０ １６８．７３ １５２．４２ １５７．４５ ３．２９
３
ｑ ４ ?（ｍ ?ｄ） ５４３．０２ ４６５．９４ ４９７．７９ １４．２９ ４９７．９１ ４９７．８７ ４９７．８１ ０．０１
３
ｑ ５ ?（ｍ ?ｄ） ４１４．４０ ３４０．０４ ３７８．９４ １３．９０ ３７９．１１ ３７９．０８ ３７８．８６ ０．０８

图 ３ 基于替代模型的 ＭＣＭＣ和两阶段的 ＭＣＭＣ反演参数的后验分布
图 ４分别为（ａ）参数 Ｋ 标准场、（ｂ）反演前随机生成的初始参数场、（ｃ）基于替代模型和（ｄ）两阶
３
段的 ＭＣＭＣ反演 Ｋ 参数场。基于替代模型和两阶段的 ＭＣＭＣ反演参数场与参数标准场之间的 ＲＭＳＥ
３
－ ２
－ ２
分别为 ８．３ × １０ 和 ２．６ × １０ ；ＳＳＩＭ分别为 ０．８８和 ０．９８，两种方法反演的参数场都较为准确，但两阶段
的 ＭＣＭＣ反演的参数场精度更高。说明仅使用替代模型的 ＭＣＭＣ参数反演，虽然计算费时少，但替
代模型的误差影响反演参数值的可靠性。而两阶段的 ＭＣＭＣ通过第一阶段缩小参数范围，第二阶段再
调用数值模型，可在实现减小计算成本的同时提高反演参数的精度。
３．３ 基于 ＥＳ － ＭＤＡ方法的参数反演 在使用 ＥＳ － ＭＤＡ方法反演地下水模型参数过程中，存在某些超
），直接影响同化算法对模型参数的更新效果。本
ａ
参数的选择（如同化次数 Ｎ、集合样本 Ｎ、膨胀系数 α ｉ
＝ ＝ ２，采用模型参数的先验分布（表 １），使用 ＥＳ － ＭＤＡ方
文借鉴前人经验 ［１６］ ，取 Ｎ ＝ ２，Ｎ ＝ １００，α １ α ２
ａ
法反演模型参数的后验分布。
ＥＳ － ＭＤＡ两次同化反演参数结果的对比见表 ４，以 ｑ、ｑ、ｑ 为例，反演参数后验分布见图 ５。
１ ２ ３
第一、二次同化反演结果各参数均值与表 １中参数真值十分接近。但第二次同化各参数均值与真值更
为接近，且标准差均小于第一次同化标准差，反演的后验分布峰值位于真值附近（图 ５）。
表 ４ ＥＳ － ＭＤＡ两次同化模型参数统计值

第一次同化 第二次同化
参数
最大值 最小值 均值 标准差 最大值 最小值 均值 标准差
３
ｑ １ ?（ｍ ?ｄ） ２７８．１５ １８７．７９ ２２６．６１ １９．４３ ２８２．４４ １９４．３６ ２２７．２６ １８．７２
３
ｑ ２ ?（ｍ ?ｄ） ２１５．８５ １５６．２７ １８３．９５ １２．４２ ２０８．７８ １５８．７１ １８１．３０ １０．７３
３
ｑ ３ ?（ｍ ?ｄ） ２２０．７０ １４５．０４ １６４．３６ １１．４０ １９２．８５ １５０．７１ １６１．４７ ５．９０
３
ｑ ４ ?（ｍ ?ｄ） ５１６．６２ ４７１．３３ ４９８．４１ ９．４８ ５１９．８７ ４６９．４３ ４９８．５０ ９．７３
３
ｑ ５ ?（ｍ ?ｄ） ４００．４６ ３５９．９１ ３８３．４０ ８．７９ ４００．３４ ３６１．５４ ３８２．５４ ８．８５

４
— １ ２ ２ —