Page 105 - 2023年第54卷第10期

逐日水头，作为参数反演的观测值。后续将 １０个监测井的模拟值与观测值的误差最小作为目标函数，
使用基于 ＭＣＭＣ和 ＥＳ － ＭＤＡ方法反演模型参数。
３．１．２ 反演参数的选择及替代模型 假设第一承压含水层渗透系数 Ｋ 的自然对数空间变化且符合 Ｋ － Ｌ
３
５ !
展开的随机场，设定 ｌｎＫ 均值为 ０，方差为 ０．５。当 Ｎ ＝ ５ ，可以保留 ７０％变异性，即 ∑ λ ｉ∑
? λ ｉ ≈ ７０％，
ＫＬ
３
ｉ ＝ １ ｉ ＝ １
）（表 １）。选择 ５个开采井开采量（ｑ，ｑ，ｑ，ｑ，ｑ）
由此生成的高斯随机数为（ ξ １ ，ξ ２ ，ξ ３ ，ξ ４ ，ξ ５ １ ２ ３ ４ ５
， ， ］，各参数取值范围和真
１ ２ ３ ４ ５
作为未知变量。待反演的参数集 θ ＝ ［ｑ，ｑ，ｑ，ｑ，ｑ，ξ １ ，ξ ２ ，ξ ３ ξ ４ ξ ５
值见表 １，其中各参数先验分布为均匀分布，各开采井开采量见表 ２。
表 １ 参数的先验分布区间和真值
３
３
３
３
ｑ １ ?（ｍ?ｄ） ｑ ２ ?（ｍ ?ｄ） ｑ ３ ?（ｍ ?ｄ） ｑ ４ ?（ｍ ?ｄ） ｑ ５ ?（ｍ ?ｄ） ξ １ ξ ２ ξ ３ ξ ４ ξ ５
区间 ［１００，３００］［１００，３００］［１００，３００］［３００，６００］［３００，６００］ ［ － １ ，１］ ［ － １ ，１］ ［ － １ ，１］ ［ － １ ，１］ ［ － １ ，１］
真值 ２２０ １８０ １６０ ５００ ３８０ ０．２９５ ０．４１５ ０．１３４ － ０．７８５ ０．４８５
３
根据 Ｋｒｉｇｉｎｇ法 建 立替 代模 型的 步骤，使 用拉丁 表 ２ 开采井开采量 单位：ｍ ?ｄ
超立方抽样 方 法 从参数 的 先 验 分 布 （表 １）均 匀 抽 取
Ｗ１ Ｗ２ Ｗ３ Ｗ４ Ｗ５
１０００组参 数，调用 ＭＯＤＦＬＯＷ 模 拟得 到 监 测 井 不 同
潜水含水层 ０ ０ ０ ｑ ４ ０
参数取值对应的水头，建立每个监测井地下水水头的
第一承压含水层 ｑ １ ｑ ２ ｑ ３ ０ ０
Ｋｒｉｇｉｎｇ替代模型；重新随机抽取 １００组参数作为检验
第二承压含水层 ０ ０ ０ ０ ｑ ５
样本的输入值，对比 １０个监测井地下水数值模型和
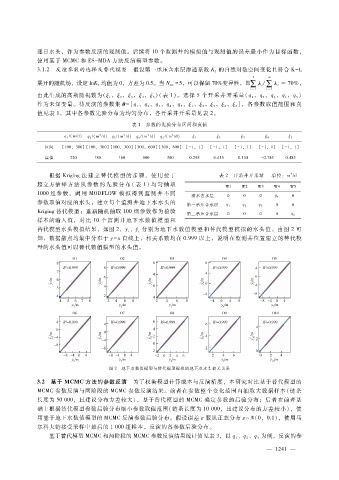
替代模型水头模拟结果，如图 ２，ｙ、 ＾ｙ分别为地下水数值模型和替代模型模拟的水头值。由图 ２可
ｉ
ｉ
知，数据散点均集中分布于 ｙ ＝ ｘ直线上，相关系数均在 ０．９９９以上，说明在监测井位置建立的替代模
型的水头值可以替代数值模型的水头值。

图 ２ 地下水数值模型与替代模型模拟的地下水水头相关关系

３．２ 基于 ＭＣＭＣ方法的参数反演 为了权衡模型计算成本与反演精度，本研究对比基于替代模型的
ＭＣＭＣ参数反演与两阶段的 ＭＣＭＣ参数反演结果。前者在参数整个变化范围内抽取大数据样本（链条
长度为 ５００００，且建议分布方差较大），基于替代模型的 ＭＣＭＣ确定参数的后验分布；后者在前者基
础上根据替代模型参数后验分布缩小参数取值范围（链条长度为 １００００，且建议分布的方差较小），使
用基于地下水数值模型的 ＭＣＭＣ反演参数后验分布。假设误差 ε 服从正态分布 ε ～Ｎ（０，０．１），使用马
尔科夫链接受采样中最后的 １０００组样本，反演的各参数后验分布。
基于替代模型 ＭＣＭＣ和两阶段的 ＭＣＭＣ参数反演结果统计值见表 ３，以 ｑ、ｑ、ｑ 为例，反演的参
１ ２ ３
２
— １ ４ １ —