Page 87 - 2023年第54卷第11期

地潜力。根据发展趋势改造为居民用地，改造面积方案分别为：（１）改造面积占比 ０．５６％（Ｃ１）；（２）
改造面积占比 ０．３０％（Ｃ２）；（３）改造面积占比 ０．１９％（Ｃ３）。
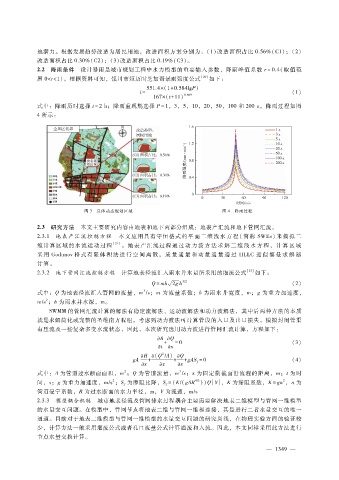
２．２ 降雨条件 设计暴雨是城市规划工程中水力模型的重要输入参数，降雨峰值系数 ｒ ＝ ０．４ （取值范
围 ０＜ｒ＜１）。根据资料可知，银川市短历时芝加哥暴雨强度公式 ［２０］ 如下：
５５１．４ × （１ ＋ ０．５８４ｌｇＰ）
ｉ ＝ （１）
１６７ × （ｔ ＋ １１ ） ０．６６９
式中：降雨历时选择 ｔ ＝ ２ｈ；降雨重现期选择 Ｐ ＝ １，３，５，１０，２０，５０，１００和 ２００ａ。降雨过程如图
４所示：

图 ３ 具体动态规划区域 图 ４ 降雨过程

２．３ 研究方法 本文主要研究内容由地表和地下两部分组成：地表产汇流和地下管网汇流。
２．３．１ 地表产汇流控制方程 本文应用具有守恒格式的平 面 二 维 浅 水 方 程 （简 称 ＳＷＥｓ）来 模 拟 二
维计算区域的水流运动过程 ［２１］ 。地表产汇流过程 通 过 动 力 波 方 法 求 解 二 维 浅 水 方 程， 计 算 区 域
采用 Ｇｏｄｕｎｏｖ格式有限 体 积 法 进 行 空 间 离 散。 质 量 通 量 和 动 量 通 量 通 过 ＨＬＬＣ近 似 黎 曼 求 解 器
计算。
２．３．２ 地下管网汇流控制方程 计算地表径流汇入雨水井水量所采用的堰流公式 ［２２］ 如下：
３?２
Ｑ ＝ ｍｂ ２ｇｈ （２）
槡
３
式中：Ｑ为地表径流汇入管网的流量，ｍ ?ｓ；ｍ为流量系数；ｂ为雨水井宽度，ｍ；ｇ为重力加速度，
２
ｍ?ｓ；ｈ为雨水井水深，ｍ。
ＳＷＭＭ的管网汇流计算的解法有稳定流解法、运动波解法和动力波解法，其中后两种方法的本质
就是求解简化或完整的圣维南方程组。考虑到动力波法可计算管段的入口及出口损失，模拟封闭管渠
有压流及一些复杂多变水流状态，因此，本次研究选用动力波进行管网汇流计算，方程如下：
 Ａ  Ｑ
＋ ＝ ０ （３）
 ｔ  ｘ
２
 Ｈ  （Ｑ ?Ａ）  Ｑ
ｇＡ ＋ ＋ ＋ ｇＡＳ＝ ０ （４）
ｆ
 ｘ  ｘ  ｘ
３
２
式中：Ａ为管道过水断面面积，ｍ ；Ｑ为管道流量，ｍ ?ｓ；ｘ为固定横截面沿流程的距离，ｍ；ｔ为时
２
２
４?３
间，ｓ；ｇ为重力加速度，ｍ?ｓ；Ｓ为摩阻比降，Ｓ＝ （Ｋ?（ｇＡＲ ））Ｑ Ｖ，Ｋ为滞阻系数，Ｋ ＝ ｇｎ，ｎ为
ｆ
ｆ
管道曼宁系数，Ｒ为过水断面的水力半径，ｍ，Ｖ为流速，ｍ?ｓ
２．３．３ 模型耦合机制 城市地表径流及管网排水过程耦合主要需要解决地表二维模型与管网一维模型
的水量交互问题。在模型中，管网节点将地表二维与管网一维相连接，其是进行二者水量交互的唯一
通道。目前对于地表二维模型与管网一维模型的水量交互问题的研究尚浅，在物理实验方面的验证较
少，计算方法一般采用堰流公式或者孔口流量公式计算溢流和入流。因此，本文同样采用此方法进行
节点水量交换计算。
３
— １ ４ ９ —