Page 93 - 2023年第54卷第12期

值得注意的是，虽然对数公式也能较好预测冰盖流纵向时均流速的垂向分布，但流速分布曲线
在最大流速位置处是不光滑的（见图 ２），即在河床区与冰盖区交界面处不满足流速梯度连续，违背
了水力学知识中的液体连续介质假定。这一结果主要是将明渠流 Ｐｒａｎｄｔｌ对 数 流速 公 式 直接拓展到
冰盖流中造成的。下面，从理论角度证 实对数 流速公式梯 度不 连续 这 一 结论。通 过 对式 （ １）求 导，
可得：
河床区（ ０＜ｚ ≤ｈ）：
ｂ
ｄＵ ｂ ｕ ｂ
＝ （２４）
ｄｚ κ ｚ
冰盖区（ｈ≤ｚ＜Ｈ）：
ｂ
ｄＵ ｕ
ｉ ｉ
＝－ （２５）
ｄｚ κ （Ｈ － ｚ）
由式（ ２４）（２５）易知，河床区的流速梯度 ｄＵ ?ｄｚ具有正值，而冰盖区的流速梯度 ｄＵ ?ｄｚ具有负值。因
ｂ ｂ
ｄＵ ｂ ｄＵ ｉ
此，在交界面 ｚ＝ｈ处， ≠ 。这一结果表明对数流速分布曲线在河床区和冰盖区交界
ｂ
ｄｚ ｄｚ
ｚ ＝ ｈ ｂ ｚ ＝ ｈ ｂ
面处难以满足连续光滑条件。
虽然双幂律流速公式克服了对数流速公式在最大流速位置处梯度不连续的缺点，但该公式未明确
涉及冰盖区与河床区的速度和长度尺度，物理意义不直观，并且公式中的 Ｋ值是根据经验进行率定
０
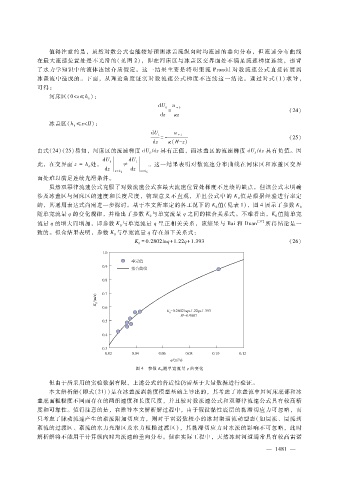
的，其通用表达式尚需进一步探讨。基于本文所率定的各工况下的 Ｋ值（见表 １），图 ４展示了参数 Ｋ
０ ０
随单宽流量 ｑ的变化规律，并给出了参数 Ｋ与单宽流量 ｑ之间的拟合关系式。不难看出，Ｋ值随单宽
０
０
流量 ｑ的增大而增加，即参数 Ｋ与单宽流量 ｑ呈正相关关系，该结果与 Ｂａｉ和 Ｄｕａｎ ［３７］ 所得结论是一
０
致的。拟合结果表明，参数 Ｋ与单宽流量 ｑ存在如下关系式：
０
Ｋ ＝ ０ ．２８０２ｌｎｑ ＋ １ ．２２ｑ ＋ １ ．３９３ （２６）
０

图 ４ 参数 Ｋ ０ 随单宽流量 ｑ的变化

但由于所采用的实验数据有限，上述公式的普适性仍需基于大量数据进行验证。
本文解析解（即式（２１））是在冰盖流涡黏度模型基础上导出的，其考虑了冰盖流中因河床底部和冰
盖底面粗糙度不同而存在的两组速度和长度尺度，并且较对数流速公式和双幂律流速公式具有较高精
度和可靠性。值得注意的是，在推导本文解析解过程中，由于假设黏性底层的黏滞切应力可忽略，而
只考虑了脉动流速产生的紊流附加切应力，则对于雷诺数较小的冰封渠道流动型态（如层流、层流到
紊流的过渡区、紊流的水力光滑区及水力粗糙过渡区），其黏滞切应力对水流的影响不可忽略，此时
解析解将不能用于计算纵向时均流速的垂向分布。但在实际工程中，天然冰封河道通常具有较高雷诺

４
— １ ８ １ —