Page 28 - 2024年第55卷第2期
P. 28
渗墙精细分析模型,并采用增量迭代法进行求解。
计算采用大连理工大学自主研发的大型岩土工程高性能分析软件系统 GEODYNA,该软件已集成
了有限元- 比例边界元- 无网格- 离散元耦合的多数值分析方法,有中点增量法、增量迭代法、等效线
性方法等隐式求解方法和显式求解方法,已广泛应用于土石坝的静、动力分析 [23 - 24,27 - 33] 。
土体采用非线性弹性邓肯张 E - μ模型,坝体和覆盖层材料的计算参数见表 1。在防渗墙与覆盖层
土体、心墙与过渡料、心墙与防渗墙之间设置 Goodman接触单元,采用双曲线模型描述其接触特性,
参数见表 2。
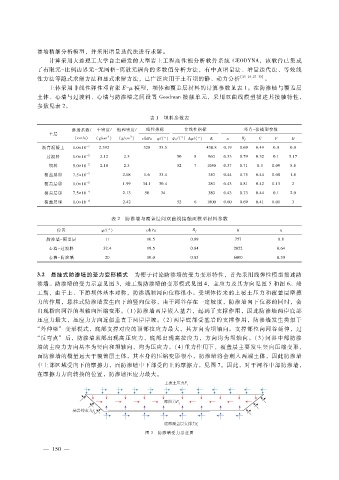
表 1 坝料参数表
渗透系数? 干密度? 饱和密度? 线性指标 非线性指标 邓肯- 张模型参数
土层
3
3
(cm?s) (g?cm ) (g?cm ) c?kPa φ ?(°) φ 0 ?(°) Δφ ?(°) K n R f G F D
沥青混凝土 1.0 × 10 - 7 2.392 320 33.5 438.8 0.19 0.69 0.49 0.0 0.0
过渡料 1.0 × 10 - 2 2.12 2.3 50 8 960 0.33 0.79 0.32 0.1 5.17
坝料 5.0 × 10 - 2 2.18 2.3 52 7 1050 0.37 0.71 0.3 0.09 5.8
- 3
覆盖层① 7.5 × 10 2.08 1.6 33.4 350 0.44 0.75 0.44 0.08 1.8
- 5
覆盖层② 1.0 × 10 1.99 34.1 30.4 280 0.43 0.81 0.42 0.13 2
- 4
覆盖层③ 7.5 × 10 2.13 50 34 380 0.43 0.73 0.44 0.1 2.0
- 4
覆盖层④ 1.0 × 10 2.42 52 6 1800 0.60 0.69 0.41 0.01 3
表 2 防渗墙与覆盖层间双曲线接触面模型材料参数
位置 φ ?(°) c?kPa R f K n
防渗墙- 覆盖层 11 10.5 0.89 757 0.8
心墙- 过渡料 32.4 19.5 0.84 2022 0.64
心墙- 防渗墙 20 10.0 0.85 6000 0.30
3.2 悬挂式防渗墙的受力变形模式 为便于讨论防渗墙的受力变形特性,首先采用线弹性模型描述防
渗墙。防渗墙的受力示意见图 3,竣工期防渗墙的变形模式见图 4,主应力及其方向见图 5和图 6。竣
工期,由于上、下游坝体基本对称,防渗墙顺河向位移很小。受坝体传来的上覆土压力和覆盖层摩擦
力的作用,悬挂式防渗墙发生向下的竖向位移,由于河谷存在一定坡度,防渗墙向下位移的同时,会
出现指向河谷的坝轴向压缩变形。( 1)防渗墙两岸嵌入基岩,起到了支撑作用,因此防渗墙两岸底部
压应力最大,压应力方向近似垂直于两岸岸坡。(2)两岸底部受基岩的支撑作用,防渗墙发生类似于
“外伸梁” 变形模式,底部支撑对应的顶部拉应力最大,其方向为坝轴向。支撑部位向河谷延伸,过
“反弯点” 后,防渗墙顶部出现高压应力,底部出现高拉应力,方向均为坝轴向。(3)河谷中部防渗
墙的主应力方向基本为竖向和坝轴向,均为压应力。( 4)重力作用下,覆盖层主要发生竖向压缩变形,
而防渗墙的模量远大于覆盖层土体,其本身的压缩变形很小,防渗墙将会刺入两端土体,因此防渗墙
中上部区域受向下的摩擦力,而防渗墙中下部受向上的摩擦力,见图 7。因此,对于河谷中部防渗墙,
在摩擦力方向转换的位置,防渗墙压应力最大。
图 3 防渗墙受力示意图
— 1 5 —
0