Page 127 - 2024年第55卷第3期

表 ２ 堰塞坝寿命预测模型
堰塞坝寿 坝体材料系数 α 坝体诱因系数 β
堰塞坝寿命各阶段预测模型 案例数
命阶段预 Ｒ ２ 渐进式 人为
及完整寿命预测模型 （个） 土质坝 土石坝 堆石坝 地震 降雨 融雪
测模型 削弱 原因
－ １２．９７８ ＋ ０．２９１Ｐｉ ＋ ２９４ ．６６２ ×
蓄水阶段 Ｔ ｉ ＝ Ｖ ｄ １?３ Ｈ ｄ １９ ０．９２６ ９．４９９ ０．０００ ０．０６９ ０．０００ － ８．４６７ － １０．８１ － １６．６１ ２７．２５
－ ０．１４７ × ＋ α ＋ β
Ｈ ｄ Ｈ ｒ
１．４３３ － ２ ．８５８
Ｈ ｄ
Ｗ ｄ
－ ９
＝
×
Ｔ ｏ ３．３８ × １０ × ( ) ( ) ×
Ｈｒ
溢流阶段 Ｈ ｄ １８ ０．９７０ １８．７８０ ４２．９２６ ６１．７０６ ０．１７７ ０．３７９ ０．６８３ ０．７８４ ２．５３２
１?３ ２４．０７７ Ｖ ｌ － １４ ．１２６
１?３
( ) ( ) ｅｅ
Ｖ ｄ
α β
×
Ｈ ｄ Ｈ ｄ
１．４２１４ Ｗ ｄ － ０ ．６４
( ) ( )
Ｈ ｄ
Ｔ ｂ ２ ．５７６ × × ×
＝
Ｈｒ
溃决时长 Ｈ ｄ １８ ０．９０８ ２．３５０ １．８６１ ３．２１９ － ０．４１２ ０．８０５ － １．２３８ － １．２３８ － １．２３８
１?３ ０．６６６ １?３ １．５６４
( ) ( ) ｅｅ
Ｖ ｌ
Ｖ ｄ
α β
×
Ｈ ｄ Ｈ ｄ
＋ ＋
完整寿命 Ｔ ＝ Ｔ ｉ Ｔ ｏ Ｔ ｂ １８ ０．９５１

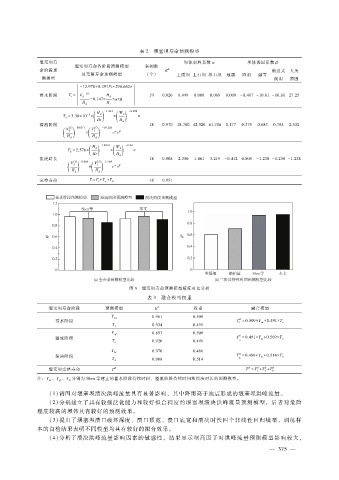
图 ８ 堰塞坝寿命预测模型精度对比分析
表 ３ 融合模型权重
堰塞坝寿命阶段 预测模型 Ｒ ２ 权重 融合模型
０．９６１ ０．５０９
Ｙ ｉｎ
Ｒ
＝
＋
蓄水阶段 Ｔ ｉ ０ ．５０９ × Ｙ ｉｎ ０ ．４９１ × Ｔ ｉ
０．９３４ ０．４９１
Ｔ ｉ
０．８５７ ０．５０９
Ｙ ｏｆ
Ｒ ＋
溢流阶段 Ｔ ＝ ０．４９１ × Ｙ ｏｆ ０．５０９ × Ｔ ｏ
０．９２６ ０．４９１ ｏ
Ｔ ｏ
０．９７０ ０．４８６
Ｙ ｂｒ
Ｒ ＋
溃决阶段 Ｔ ＝ ０．４８６ × Ｙ ｂｒ ０．５１４ × Ｔ ｂ
０．９０８ ０．５１４ ｂ
Ｔ ｂ
Ｒ
Ｒ
Ｒ
Ｒ
堰塞坝完整寿命 Ｔ Ｒ Ｔ ＝ Ｔ ｉ Ｔ ｏ Ｔ ｂ
＋ ＋
注：Ｙ ｉｎ 、Ｙ ｏｆ 、Ｙ ｂｒ 分别为 Ｓｈｅｎ等建立的蓄水阶段持续时间、溢流阶段持续时间和溃决时长的预测模型。
（１）诱因对堰塞坝溃决洪峰流量具有显著影响，其中降雨高于地震形成的堰塞坝洪峰流量。
（２）分别建立了具有较强泛化能力和较好拟合程度的堰塞坝溃决洪峰流量预测模型，后者对危险
程度较高的坝体具有较好的预测效果。
（ ３）提出了堰塞坝溃口破坏深度、溃口顶宽、溃口底宽和溃决时长四个非线性回归模型，训练样
本的自检结果表明不同模型均具有较好的拟合效果。
（ ４）分析了溃决洪峰流量影响因素的敏感性，结果显示坝高因子对洪峰流量预测模型影响较大，
— ３ ７ ５ —