Page 126 - 2024年第55卷第3期

率及坝体渗流率的影响，可将蓄水过程简化为一个线性问题，建立朴素模型 Ｐ如下：
６
６
１０× Ｖ ｌ １０× Ｖ ｌ
Ｐ ＝ （４） Ｐ＝ （５）
ｉ
８６４００ × （Ｑ － Ｓ） ８６４００ × Ｑ ｉｎ
ｉｎ
３
３
式中：Ｑ 为入流率，ｍ ?ｓ；Ｓ为渗流率，ｍ ?ｓ。由于渗流率未被统计，且其影响较小，用式（５）模型
ｉｎ
替代。此外，诱因也对蓄水阶段有一定影响，地震余震导致的内部结构突变可改变渗流状态，暴雨通
常会增大上游入流率。为提高模型的预测效果，基于式（ ５）、坝高因子、坝体形状和诱因建立了蓄水
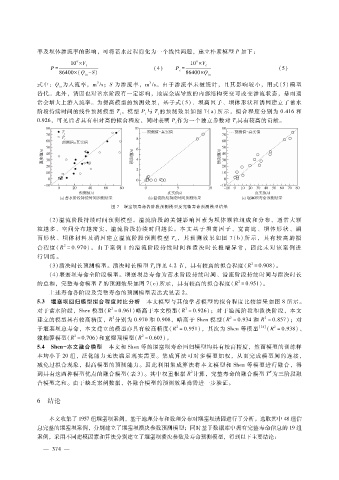
阶段持续时间的线性预测模型 Ｔ。模型 Ｐ与 Ｔ的预测效果如图 ７（ａ）所示，拟合程度分别为 ０．４１６和
ｉ ｉ ｉ
０．９２６，可见后者具有相对高的拟合程度，同时表明 Ｐ作为一个独立参数对 Ｔ具有较高的贡献。
ｉ ｉ

图 ７ 堰塞坝寿命各阶段预测模型及完整寿命预测模型结果

（２）溢流阶段持续时间预测模型。溢流阶段的关键影响因素为坝体颗粒组成和分布，通常大颗
粒越多、空间分布越密实，溢流阶段持续时间越长。本 文 基 于 坝 高 因 子、 宽 高 比、 坝 体 形 状、 湖
面形状、坝体材料及诱因建立溢流阶段预测模 型 Ｔ，其 预 测 效 果 如 图 ７（ｂ）所 示， 具 有 较 高 的 拟
ｏ
２
合程度（ Ｒ ＝ ０．９７０）。由于案例 １的溢流阶段持 续 时 间 和 溃 决 时 长 极 端 异 常， 因 此 未 对 该 案 例 进
行训练。
２
（ ３）溃决时长预测模型。溃决时长模型 Ｔ详见 ４．２节，具有较高的拟合程度（Ｒ ＝ ０．９０８ ）。
ｂ
（４）堰塞坝寿命全阶段模型。堰塞坝总寿命为蓄水阶段持续时间、溢流阶段持续时间与溃决时长
２
的总和，完整寿命模型 Ｔ的预测效果如图 ７（ｃ）所示，具有较高的拟合程度（Ｒ ＝ ０．９５１ ）。
上述寿命各阶段及完整寿命的预测模型表达式见表 ２。
５．３ 堰塞坝回归模型拟合程度对比分析 本文模型与其他学者模型的拟合程度比较结果如图 ８所示。
２
２
对于蓄水阶段，Ｓｈｅｎ模型（Ｒ ＝ ０．９６１）略高于本文模型（Ｒ ＝ ０．９２６）；对于溢流阶段和溃决阶段，本文
２
２
２
建立的模型具有较高精度，Ｒ分别为 ０．９７０和 ０．９０８，略高于 Ｓｈｅｎ模型（Ｒ ＝ ０．９３４和 Ｒ ＝ ０．８５７ ）；对
２
２
于堰塞坝总寿命，本文建立的模型亦具有较高精度（ Ｒ ＝ ０．９５１ ），其次为 Ｓｈｅｎ等模型 ［１４］ （Ｒ ＝ ０．９３８ ）、
２
２
赖柏蓉模型（Ｒ ＝ ０．７０６ ）和童煜翔模型（Ｒ ＝ ０．６０３ ）。
５．４ Ｓｈｅｎ － 本文融合模型 本文和 Ｓｈｅｎ等的堰塞坝寿命回归模型均具有较高精度，然而模型的训练样
本均小于 ２０组，泛化能力无法满足现实需要。集成算法可对多模型加权，从而完成模型间的连接，
减免过拟合现象，提高模型的预测能力。因此利用集成算法将本文模型和 Ｓｈｅｎ等模型进行融合，得
Ｒ
２
到具有这两种模型优点的融合模型（表 ３）。其中权重根据 Ｒ计算，完整寿命的融合模型 Ｔ为三阶段融
合模型之和。由于缺乏案例数据，各融合模型的预测效果尚需进一步验证。
６ 结论

本文收集了 １９５７组堰塞坝案例，基于地理分布和数理分布对堰塞坝诱因进行了分析。选取其中 ４８组信
息完整的堰塞坝案例，分别建立了堰塞坝溃决参数预测模型；同时基于数据库中拥有完整寿命信息的 １９组
案例，采用不同建模因素和算法分别建立了堰塞坝溃决参数及寿命预测模型，得到以下主要结论：

４
— ３ ７ —