Page 121 - 2024年第55卷第3期

定、溃决参数及寿命的预测中 ［７，１１，１４］ 。本文主要采用 ４个无量纲参数，其中坝高因子（Ｈ ?Ｈ）反映堰塞
ｄ ｒ
坝几何形态及库区潜在水量，坝高 Ｈ单位为 ｍ，Ｈ ＝ １ｍ ，用以消除量纲影响；宽高比（Ｗ ?Ｈ）反映堰塞
ｄ ｒ ｄ ｄ
１?３
坝堆积形态及水力梯度，坝宽 Ｗ 单位为 ｍ；坝体形状系数（Ｖ ?Ｈ ）反映堰塞坝堆积形态及抗冲蚀能力，
ｄ
ｄ
ｄ
６
３
１?３
３
６
坝体积 Ｖ单位为 １０ｍ ；湖面形状系数（Ｖ ?Ｈ）反映堰塞坝库区水文状态，其中库容 Ｖ单位为 １０ｍ 。
ｄ ｌ ｄ ｌ
４ 溃决参数预测
４．１ 洪峰流量预测模型 洪峰流量主要受坝体的颗粒级配及空间分布、几何尺寸及上游水文参数影
响 ［２３ － ２６］ 。对于含大颗粒较多的坝体，水流侵蚀可裹挟的物料少，溃口发展程度低，易出现稳定透水现
象，从而抑制洪峰流量的发展 ［２７ － ３０］ 。对于高度较高、体积较大的坝体，上游来水量、蓄水量和水流冲
击力通常较大，溢流时间较长，显著影响溃口演化和洪峰流量大小 ［３１ － ３２］ ；对于库容及来水量大的坝
体，通常蓄水时间较短、上游来水冲击力较强，从而也影响坝体侵蚀过程和洪峰流量 ［３３ － ３６］ 。余震可使
堰塞坝内部结构发生突变并导致坝体坍塌，从而拦水量和洪峰流量减少、峰现时间提前 ［２３］ 。暴雨使坝
体初始含水率增大，从而水对坝体的侵蚀效率提高、溃口边坡的重力坍塌加剧；此外汇水流域暴雨可
显著提高上游来水量，洪峰流量可能增大。数据库中拥有较完整信息的案例共 ４８组，不同因素的分
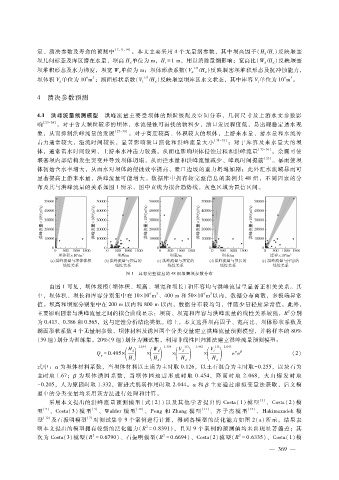
布及其与洪峰流量的关系如图 １所示，图中直线为拟合趋势线，灰色区域为置信区间。

图 １ 具有完整信息的 ４８组堰塞坝参数分布
由图 １可见，坝体规模（坝体积、坝高、坝宽和坝长）和库容均与洪峰流量呈显著正相关关系。其
６
６
３
３
中，坝体积、坝长和库容分别集中在 １０ × １０ｍ 、４００ｍ和 ５０ × １０ｍ 以内，数据分布离散，多极端异常
值。坝高和坝宽分别集中在 ２００ｍ以内和 ８００ｍ以内，数据分布较均匀，伴随少量轻度异常值。此外，
２
主要影响因素与洪峰流量之间的拟合曲线显示：坝高、坝宽和库容与洪峰流量的线性关系较强，Ｒ分别
为 ０．４１３、０．３８６和 ０．５６５，这与定性分析结论类似。综上，本文选择坝高因子、宽高比、坝体形状系数及
湖面形状系数 ４个无量纲参数，坝体材料及诱因两个分类变量建立洪峰流量预测模型，并将样本的 ８０％
（３９组）划分为训练集，２０％（９组）划分为测试集，利用非线性回归算法建立洪峰流量预测模型：
１．１９４
１．３５４
１?３ ２．０４３
１?３ － １．４４２
Ｗ
Ｖ
Ｈ
Ｖ
ｄ
ｌ
ｄ
ｄ
α β
×
×
×
Ｑ ＝ ０．４９５ × ( ) ( ) ( ) ( ) ｅｅ （２）
ｐ Ｈ Ｈ Ｈ Ｈ
ｒ ｄ ｄ ｄ
式中：α为坝体材料系数，当坝体材料以土质为主时取 ０．１２６，以土石混合为主时取－ ０．２５５ ，以块石为
主时取 １．６７；β为 坝 体 诱 因 系 数，当 坝 体 因 地 震 形 成 时 取 ０．４５４，降 雨 时 取 ２．０６８，火 山 爆 发 时 取
－ ０．２０５ ，人为原因时取 １．３３２，渐进式削弱作用时取 ２．０４４。α和 β主要通过虚拟变量法获取，后文模
型中的分类变量均采用该方法进行处理和计算。
采用本文提出的洪峰流量预测模型（式（ ２））以及其他学者提出的 Ｃｏｓｔａ（１）模型 ［３］ 、Ｃｏｓｔａ（２）模
型 ［３］ 、Ｃｏｓｔａ（３）模 型 ［３］ 、Ｗａｌｄｅｒ模 型 ［１０］ 、Ｐｅｎｇ和 Ｚｈａｎｇ模 型 ［１１］ 、齐 子 杰 模 型 ［１３］ 、Ｈａｋｉｍａｚａｄｅｈ模
型 ［１２］ 及石振明模型 ［７］ 对测试集中 ９个案例进行计算，得到各模型的泛化能力如图 ２（ａ）所示。结果表
２
明本文提出的模型拥有较强的泛化能力（Ｒ ＝ ０．８３９１ ），且对 ９个案例的预测值均未出现显著偏差；其
２
２
２
次为 Ｃｏｓｔａ（３）模型（Ｒ ＝ ０．６７９０ ）、石振明模型（Ｒ ＝ ０．６６９４ ）、Ｃｏｓｔａ（２）模型（Ｒ ＝ ０．６３３５ ）、Ｃｏｓｔａ（１）模
— ３ ６ ９ —