Page 127 - 2024年第55卷第5期

性。该电站孤网模式下数据如表 １示。
表 １ 某水电站 ＨＴＲＳ参数

子系统 参数
＝
＝
＝
ＰＩＤ控制器 Ｋ Ｐ ２．８，Ｋ Ｉ ０．２，Ｋ Ｄ ０
＝
随动系统 Ｔ ｙ ０．４５９４
３
＝
＝
＝
＝
水轮机 Ｄ＝ ６．２２３ｍ，Ｈ ｒ １９７ｍ，最大水头 Ｈ ｍａｘ ２２９．４ｍ，最小水头 Ｈ ｍｉｎ １５４．６ｍ，Ｑ ｒ ４３２．７ｍ ?ｓ
＝
引水系统 Ｔ ｗ １．２９
＝
＝
＝
发电机 Ｔ ａ １２．２３９ ，ｅ ｇ ０．１７６ ，Ｘ ｒ １２５
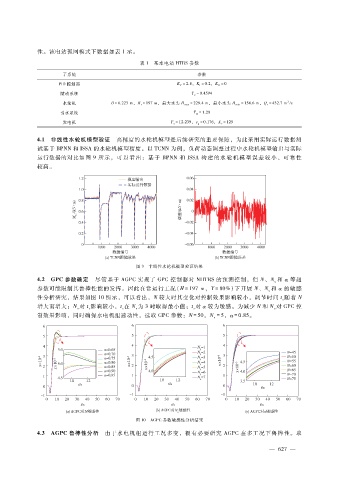
４．１ 非线性水轮机模型验证 高精度的水轮机模型是后续研究的重要保障，为此采用实际运行数据测
试基于 ＢＰＮＮ和 ＩＳＳＡ的水轮机模型精度。以 ＴＣＮＮ为例，负荷动态调整过程中水轮机模型输出与实际
运行数据的对比如图 ９所 示，可 以看 出：基于 ＢＰＮＮ和 ＩＳＳＡ构 建 的水 轮 机 模型 误差 较小、可靠性
较高。

图 ９ 非线性水轮机模型验证结果

４．２ ＧＰＣ参数确定 尽管基于 ＡＧＰＣ实现了 ＧＰＣ控制器对 ＮＨＴＲＳ的预测控制，但 Ｎ、Ｎ 和 α等超
ｕ
参数可能限制其鲁棒性能的发挥。因此在常运行工况（Ｈ＝ １９７ｍ，Ｙ ＝ ８０％）下开展 Ｎ、Ｎ 和 α的敏感
ｕ
性分析研究，结果如图 １０所示，可以看出，Ｎ较大时其变化对控制效果影响较小，调节时间 ｔ随着 Ｎ
ｓ
增大而增大；Ｎ对 ｔ影响较小，ｔ在 Ｎ 为 ３时取得最小值；ｔ对 α较为敏感。为减少 Ｎ和 Ｎ 对 ＧＰＣ控
ｕ ｓ ｓ ｕ ｓ ｕ
制效果影响，同时确保水电机组速动性，选取 ＧＰＣ参数：Ｎ ＝ ５０，Ｎ ＝ ５，α ＝ ０．８５。
ｕ

图 １０ ＡＧＰＣ参数敏感性分析结果
４．３ ＡＧＰＣ鲁棒性分析 由于水电机组运行工况多变，极有必要研究 ＡＧＰＣ在多工况下鲁棒性。取

— ６ ２ ７ —