Page 123 - 2024年第55卷第5期

ｙ Ｋ ｙ
Ｇ（ｓ） ＝ ＝ （１１）
ｅ ２
ｕ Ｔ Ｔｓ ＋ Ｔｓ ＋ Ｋ
ｙ１ ｙ ｙ ｙ

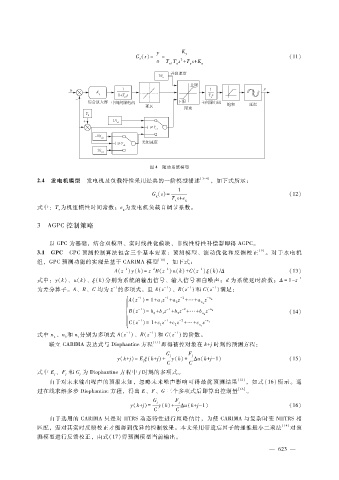
图 ４ 随动系统模型

２．４ 发电机模型 发电机及负载特性采用经典的一阶模型描述 ［３ － ４］ ，如下式所示：
１
Ｇ（ｓ） ＝ （１２）
ｇ
Ｔｓ ＋ ｅ
ａ ｇ
式中：Ｔ为机组惯性时间常数；ｅ为发电机负载自调节系数。
ａ ｇ
３ ＡＧＰＣ控制策略

以 ＧＰＣ为基础，结合双模型、实时线性化模块、非线性特性补偿器即得 ＡＧＰＣ。
３．１ ＧＰＣ ＧＰＣ预测控制算法包含三个基本要素：预测模型、滚动优化和反馈校正 ［９］ 。对于水电机
组，ＧＰＣ预测功能的实现是基于 ＣＡＲＩＭＡ模型 ［１０］ ，如下式：
－ １ － ｄ － １ － １
Ａ（ｚ ）ｙ（ｋ） ＝ｚ Ｂ（ｚ ）ｕ（ｋ） ＋ Ｃ（ｚ ） ξ （ｋ）? Δ （１３）
－ １
式中：ｙ（ｋ）、ｕ（ｋ）、ξ （ｋ）分别为系统的输出信号、输入信号和白噪声；ｄ为系统延时阶数；Δ ＝ １ － ｚ
－ １
－ １
－ １
－ １
为差分算子。Ａ、Ｂ、Ｃ均为 ｚ 的多项式，且 Ａ（ｚ ）、Ｂ（ｚ ）和 Ｃ（ｚ ）满足：
－ １
－ ２
－ １
Ａ（ｚ ） ＝１ ＋ ａｚ ＋ ａｚ ＋ …＋ ａ ｚ
－ ｎ ａ
２
１
ｎ ａ
－ １ － １ － ２ － ｎ ｂ
Ｂ（ｚ ） ＝ｂ＋ ｂｚ ＋ ｂｚ ＋ …＋ ｂ ｚ （１４）
０ １ ２ ｎ ｂ
－ ２
－ １
－ １
Ｃ（ｚ ） ＝１ ＋ ｃｚ ＋ ｃｚ ＋ …＋ ｃｚ
－ ｎ ｃ
１ ２ ｎ ｃ
－ １
－ １
－ １
式中 ｎ、ｎ和 ｎ分别为多项式 Ａ（ｚ ）、Ｂ（ｚ ）和 Ｃ（ｚ ）的阶数。
ｃ
ｂ
ａ
联立 ＣＡＲＩＭＡ表达式与 Ｄｉｏｐｈａｎｔｉｎｅ方程 ［１１］ 即得被控对象在 ｋ ＋ ｊ时刻的预测方程：
Ｇ ｊ Ｆ ｊ
ｙ（ｋ ＋ ｊ） ＝Ｅξ （ｋ ＋ ｊ） ＋ ｙ（ｋ） ＋ Δ ｕ（ｋ ＋ ｊ － １） （１５）
ｊ
Ｃ Ｃ
式中 Ｅ、Ｆ 和 Ｇ 为 Ｄｉｏｐｈａｎｔｉｎｅ方程中 ｊ时刻的多项式。
ｊ ｊ ｊ
由于对未来输出噪声的预报未知，忽略未来噪声影响可得最优预测结果 ［１２］ ，如式（１６）所示。通
过在线求解多步 Ｄｉｏｐｈａｎｔｉｎｅ方程，得出 Ｅ、Ｆ、Ｇ三个多项式后即算出控制量 ［１３］ 。
Ｇ ｊ Ｆ ｊ
ｙ（ｋ ＋ ｊ） ＝ ｙ（ｋ） ＋ Δ ｕ（ｋ ＋ ｊ － １ ） （１６）
Ｃ Ｃ
由于选用的 ＣＡＲＩＭＡ只是对 ＨＴＲＳ动态特性进行粗略估计，为使 ＣＡＲＩＭＡ与复杂时变 ＮＨＴＲＳ相
匹配，需对其实时反馈校正才能得到优异的控制效果。本文采用带遗忘因子的递推最小二乘法 ［１４］ 对预
测模型进行反馈校正，由式（１７）得预测模型当前输出。
— ６ ２ ３ —