Page 115 - 2025年第56卷第1期
P. 115
知函数; B 为二类边界; q (x, y, z, t)为二类边界 B 上的已知函数, 当 q (x, y, z, t)= 0 时可用来
2 2 2 2
n
表示相对隔水边界; 为边界上某点(x, y, z)处外法线上的单位向量。
2.4.2 模型时空离散化 基于研究区现有资料, 本文模拟了 2017 年初到 2019 年末期间地下水流及氯
离子浓度分布的时空变化, 共设有 36 个应力期, 计算时间步长为月。 计算区面积约为 78 km , 均匀
2
剖分为 3 层 50 m×50 m 的有限差分网格, 整个模型共剖分 93 420 个计算网格。 研究区平面网格剖分如
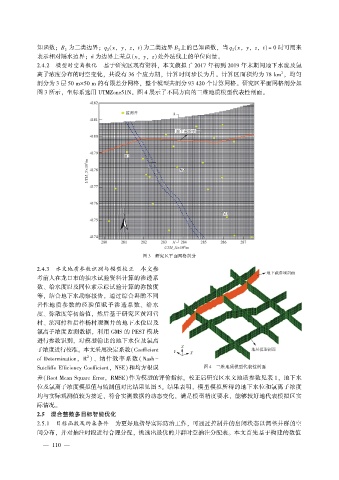
图 3 所示, 坐标系选用 UTMZone51N。 图 4 展示了不同方向的三维地质模型代表性剖面。
图 3 研究区平面网格剖分
2.4.3 水文地质参数识别与模型校正 本文参
考前人在龙口市的抽水试验资料计算的渗透系
数、 给水度以及同位素示踪试验计算的弥散度
等, 结合地下水勘察报告, 通过综合斟酌不同
岩性地质参数的经验值赋予渗透系数、 给水
度、 弥散度等初始值, 然后基于研究区黄河营
村、 滨河村和后柞杨村观测井的地下水位以及
氯离子浓度监测数据, 利用 GMS 的 PEST 模块
进行参数识别, 对模型输出的地下水位及氯离
子浓度进行校准。 本文采用决定系数(Coefficient
2
of Determination, R )、 纳什效率系数( Nash -
Sutcliffe Efficiency Coefficient, NSE)和均方根误 图 4 三维地质模型代表性剖面
差(Root Mean Square Error, RMSE)作为模型的评价指标。 校正后研究区水文地质参数见表 1, 地下水
位及氯离子浓度模拟值与监测值对比结果见图 5。 结果表明, 模型模拟所得的地下水位和氯离子浓度
均与实际观测值较为接近, 符合实测数据的动态变化, 满足模型精度要求, 能够较好地代表模拟区实
际情况。
2.5 混合整数多目标智能优化
2.5.1 目标函数及约束条件 为更好地指导实际防治工作, 可通过控制井的启闭状态以调整井群的空
间分布, 并对抽注时段进行合理分配, 挑选出最优的井群时空抽注分配表。 本文首先基于构建的数值
— 1 1 0 —