Page 117 - 2025年第56卷第1期
P. 117
刻地下坝内陆侧的盐分质量; I 为最大可供水量。 其中式(11)为研究区三维变密度地下水流和溶质运
max
移模拟模型的转化形式, 作为优化模型的等式约束条件, 从而实现模拟模型与优化模型的连接耦合。
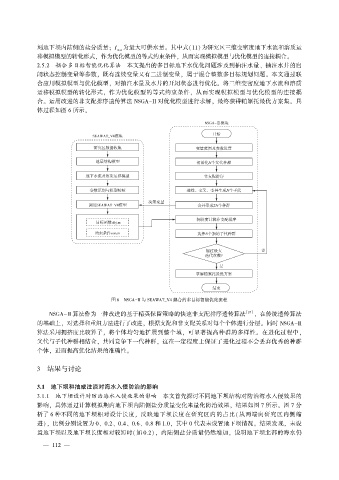
2.5.2 耦合多目标智能优化算法 本文提出的多目标地下水优化问题涉及到抽注水量、 抽注水井的启
闭状态控制变量等参数, 既有连续变量又有二进制变量, 属于混合整数多目标规划问题。 本文通过联
合应用模拟模型与优化模型, 对抽注水量及水井的开闭状态进行优化。 将三维变密度地下水流和溶质
运移模拟模型的转化形式, 作为优化模型的等式约束条件, 从而实现模拟模型与优化模型的连接耦
合。 运用改进的非支配排序遗传算法 NSGA-II 对优化模型进行求解, 最终获得帕累托最优方案集。 具
体过程如图 6 所示。
图 6 NSGA-II 与 SEAWAT_V4 耦合的多目标智能优化流程
NSGA-II 算法作为一种改进的基于精英保留策略的快速非支配排序遗传算法 [24] , 在传统遗传算法
的基础上, 对选择和重组方法进行了改进, 根据支配和非支配关系对每个个体进行分层。 同时 NSGA-II
算法采用拥挤度比较算子, 将个体均匀地扩展到整个域, 可显著提高种群的多样性。 在进化过程中,
父代与子代种群相结合, 共同竞争下一代种群, 这在一定程度上保证了进化过程不会丢弃优秀的种群
个体, 进而提高优化结果的准确性。
3 结果与讨论
3.1 地下坝和抽咸注淡对海水入侵防治的影响
3.1.1 地下坝设计对防治海水入侵效果的影响 本文首先探讨不同地下坝结构对防治海水入侵效果的
影响, 具体通过计算模拟期内地下坝内陆侧盐分质量变化来量化防治效果, 结果如图 7 所示。 图 7 分
析了 6 种不同的地下坝相对设计长度, 反映地下坝长度在研究区内的占比(从两端向研究区内侧缩
进), 比例分别设置为 0、 0.2、 0.4、 0.6、 0.8 和 1.0, 其中 0 代表未设置地下坝情况。 结果发现, 未设
置地下坝以及地下坝长度相对较短时(如 0.2), 内陆侧盐分质量仍然增加, 说明地下坝北部的海水仍
— 1 1 2 —