Page 25 - 2025年第56卷第2期

上述过程中，气泡的运动方程如下所示：
３
π ｄ π ｄ ３ １ ｔ １ ｄＵ
ａｄＵ
ａ π
２
２
） － ）ｇ Ｃ ｄ Ｕ Ｕ － Ｋ ｄ πμρ ｗ ∫ ｄ τ （１４）
（ ρ ａ ＋ Ｋ ρ ｗ ＝ （ ρ ｗ ρ ａ － ρ ｗ Ｄ ａ ａ － ｗ ａ － ｗ Ｂ ａ 槡
ｍ
６ ｄｔ ６ ８ ４ ０ ｄ τ
槡 ｔ － τ
式中：Ｋ 、Ｋ 分别为附加质量力和 Ｂａｓｓｅｔ力的经验系数；τ 为 Ｂａｓｓｅｔ力积分式的时间自变量。
ｍ
Ｂ
球形气泡直径随水深的变化关系为：
４ σ
π ３
ｇｈ ＋ ） ＝ｎＲＴ （１５）
ａ
ｄ（ｐ＋ ρ ｗ
０
６ ｄ
ａ
式中：ｐ为标准大气压，等于 １０１３５Ｐａ；ｎ为摩尔数，０℃标准大气压状态下，单位体积空气的摩尔
０
数约为 ４４．６４ｍｏｌ；Ｒ为理想气体常数，其值约为 ８．３１４Ｊ?（ｍｏｌ·Ｋ）；Ｔ为温度，单位为 Ｋ。
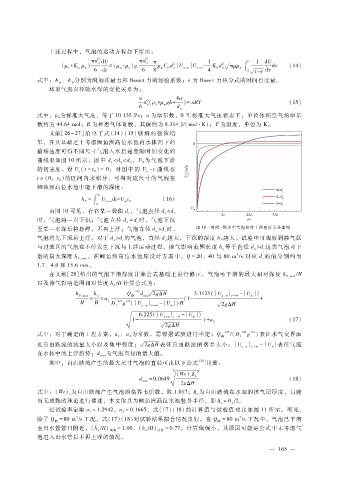
文献［２６ － ２７］给出了式 （１４）（１５）联解 的数 值结
果，在其基础之上考虑鲤鱼洲高位水池内水体向下的
输移速度可得不同尺寸气泡入水后速度随时间变化的
曲线形如图 １０所示，图中 ｄ＜ｄ＜ｄ，Ｕ 为气泡下潜
２
０
１
３
的初速度。设 Ｕ（ｔ ＝ ｔ） ＝０，对 图中 的 Ｕ － ｔ曲 线在
ａ ０ ａ
ｔ ∈（０，ｔ）的区间内求积分，可得对应尺寸的气泡在
０
鲤鱼洲高位水池中能下潜的深度：
ｔ ０
ｈ ＝ Ｕ ｄｔ － Ｕ ｔ （１６）
Ｐ ∫ ａ － ｗ
ｗ ０
０
由图 １０可见，存在某一数值 ｄ，气泡直径 ｄ＜ｄ ｃ
ｃ
ａ
时，气泡将一直下沉；气泡直径 ｄ ＝ ｄ时，气泡下沉
ａ
ｃ
至某一水深后将悬停，不再上浮；气泡直径 ｄ＞ｄ时， 图 １０ 时间－ 静水中气泡相对上浮速度关系曲线
ａ ｃ
气泡将先下沉后上浮。对于 ｄ＞ｄ的气泡，直径 ｄ越大，下沉的深度 ｈ越大。试验中可观察到掺气区
ａ ｃ ａ Ｐ
与过渡区的气泡在不停发生下沉与上浮运动过程，掺气影响范围长度 ｈ等于直径 ｄ＞ｄ这类气泡可下
ｃ
ａ
ａ
３
潜的最大深度 ｈ 。在鲤鱼洲高位水池原设计方案中，Ｑ＝ ２０、４０与 ８０ｍ ?ｓ对应 ｄ的值分别约为
Ｐ，ｍａｘ ｃ
１．７、４．０和 １５．６ｍｍ。
在文献［２８］给出的气泡下潜深度计算公式基础上进行修正，气泡可下潜的最大相对深度 ｈ Ｐ，ｍａｘ ?Ｈ
以及掺气影响范围相对长度 ｈ?Ｈ计算公式为：
ａ
ｈ ｈ Ｑ ２?３ ｄ ｍａｘ 槡 ２ｇ Δ Ｈ ３ ．１１２５（ Ｕ － Ｕ ）
Ｐ，ｍａｘ ａ 跌 ａ － ｗ ｔ →∞ ｗ
＝ ＝ ａ （１ － ＋
Ｈ Ｈ １ Ｄ ２?３ １?３ － Ｕ ）Ｈ ２ｇ Δ Ｈ
ｇ （ Ｕ
１ ａ － ｗ ｔ →∞ ｗ 槡
６ ．２２５（ Ｕ ａ － ｗ ｔ →∞ － Ｕ ）
ｗ
１ － ） ＋ ａ ２ （１７）
槡 槡 ２ｇ Δ Ｈ
ｇ ）表征水气交界面
式中：对于确定的工程方案，ａ、ａ为常数，需根据试验进行率定；Ｑ 跌 ２?３ ?（Ｄ １ ２?３ １?３
１
２
处自由跌流的流量大小以及集中程度； ２ｇ Δ Ｈ表征自由跌流的落差大小； Ｕ ａ － ｗ ｔ →∞ － Ｕ 表征气泡
槡
ｗ
在水体中的上浮趋势；ｄ 为气泡直径的最大值。
ｍａｘ
其中，自由跌流产生的最大尺寸气泡的直径可由以下公式 ［２８］ 计算：
３
２
（Ｗｅ）δ ａ
ｃ
ｄ ＝ ０ ．０６４９ （１８）
槡 ２ｇ Δ Ｈ
ｍａｘ
为自由跌流在水面的挟气层厚度，目前
式中：（ Ｗｅ）为自由跌流产生气泡的临界韦伯数，取 １．０１７；δ ａ
ｃ
＝ Ｄ ?２。
尚无成熟的理论进行描述，本文取其为鲤鱼洲高位水池竖井半径，即 δ ａ ２
经试验率定取 ａ＝ １．２９４２，ａ＝ ０．１６６５，式（１７）（１８）的计算值与试验值对比如图 １１所示。可见，
１ ２
３
３
除了 Ｑ ＝ ８０ｍ ?ｓ工况，式（１７）（１８）对试验结果拟合情况良好。在 Ｑ ＝ ８０ｍ ?ｓ工况中，气泡已下潜
跌
跌
至出水管管口附近，（ ｈ?Ｈ） ＝ １．００ ，（ｈ?Ｈ） ＝ ０．７７ ，计算值偏小，其原因可能是公式中未考虑气
ａ 试验 ａ 计算
泡进入出水管后不再上浮的情况。
— １ ６ ５ —