Page 42 - 水利学报2025年第56卷第3期

加，沉速会线性地增大。这是由公式本身的形式决定的，观察式（１）的最后一项，在不考虑清水容重
随温度变化的情况下，这一温度修正项实际上是线性的。然而，根据泥沙沉降的基本概念，在过渡区
内，泥沙颗粒粒径越大，颗粒雷诺数就越大，水流黏滞作用对其沉速的影响应该越小，冈恰诺夫早期
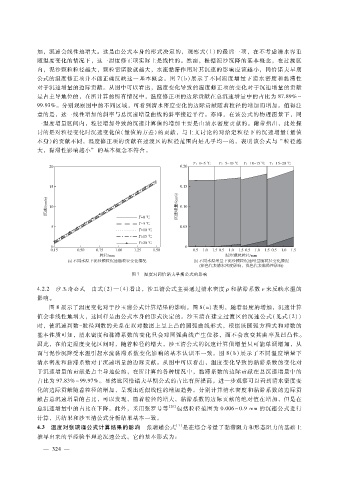
公式的温度修正项并不能正确反映这一基本概念。图 ７（ｂ）展示了不同温度增量下清水密度和黏滞性
对于沉速增量的边际贡献。从图中可以看出，温度变化导致的温度修正项的变化对于沉速增量的贡献
是占主导地位的，在所计算的所有情况中，温度修正项的边际贡献在总沉速增量中的占比为 ８７．８９％～
９９．９３％。分别观察图中的不同区域，可看到清水密度变化的边际贡献随着粒径的增加而增加。值得注
意的是，这一线性增加的斜率与总沉速增量曲线的斜率接近平行。亦即，在该公式的物理图景下，同
一温度增量区间内，粒径增加导致的沉速计算值的增加主要是由清水密度贡献的。附带指出，此处探
讨的是对粒径变化时沉速变化值（量值的方差）的贡献，与上文讨论的对给定粒径下的沉速增量（量值
本身）的贡献不同，温度修正项的贡献在过渡区的粒径范围内是几乎均一的，表明该公式与 “粒径越
大，黏滞性影响越小” 的基本概念不符合。

图 ７ 温度对冈恰诺夫早期公式的影响

４．２．２ 沙玉清公式 由式（２）—（４）看出，沙玉清公式主要通过清水密度 ρ 和黏滞系数 ν 来反映水温的
影响。
图 ８展示了温度变化对于沙玉清公式计算结果的影响。图 ８（ａ）表明，随着温度的增加，沉速计算
值会非线性地增大，这同样是由公式本身的形式决定的。沙玉清在建立过渡区的沉速公式（见式（ ２））
时，使沉速判数－ 粒径判数的关系在双对数图上呈上凸的圆弧曲线形式，根据该圆弧方程式和对数的
基本性质可知，清水密度和黏滞系数的变化只会对圆弧曲线产生位移，而不会改变其曲率及凹凸性。
因此，在给定温度变化区间时，随着粒径的增大，沙玉清公式的沉速计算值增量只可能单调增加，从
而与泥沙沉降受水温引起水流黏滞系数变化影响的基本认识不一致。图 ８（ｂ）展示了不同温度增量下
清水密度和黏滞系数对于沉速增量的边际贡献。从图中可以看出，温度变化导致的黏滞系数的变化对
于沉速增量的贡献是占主导地位的，在所计算的各种情况中，黏滞系数的边际贡献在总沉速增量中的
占比为 ９７．８３％～９９．９７％。显然比冈恰诺夫早期公式的占比有所提高。进一步观察可以看到清水密度变
化的边际贡献随着粒径的增加，呈现出近似线性的增加趋势。分别计算清水密度和黏滞系数的边际贡
献占总沉速增量的占比，可以发现，随着粒径的增大，黏滞系数的边际贡献的绝对值在增加，但是在
总沉速增量中的占比在下降。此外，采用张罗号等 ［２０］ 包括粒径范围为 ０．００６～０．９ｍｍ的沉速公式进行
计算，其结果和沙玉清公式分析结果基本一致。
４．３ 温度对张瑞瑾公式计算结果的影响 张瑞瑾公式 ［１］ 是在综合考量了黏滞阻力和形态阻力的基础上
推导出来的半经验半理论沉速公式。它的基本形式为：

４
— ３ ２ —