Page 41 - 水利学报2025年第56卷第3期

问题病态程度，在 １～３之间进行选择。本研究分别对 ４种粒径级进行了三类多项式的回归，最终采用
决定系数最大的三次多项式为本文的级配转换公式（最终的公式回归结果参见表 ５）。
ｎ
ｎ － １
ｙ ＝ ｆ（ｘ） ＝ａｘ＋ ａｘ ＋ …＋ ａｘ ＋ ａ ｎ ＋ １ （８）
１
２
ｎ
式中：ｘ为转换前的粒径组百分比含量；ｙ为转换后的粒径组百分比含量；ａ 为多项式系数，ｉ ＝ １ ，２，
ｉ
…，ｎ ＋ １ 。
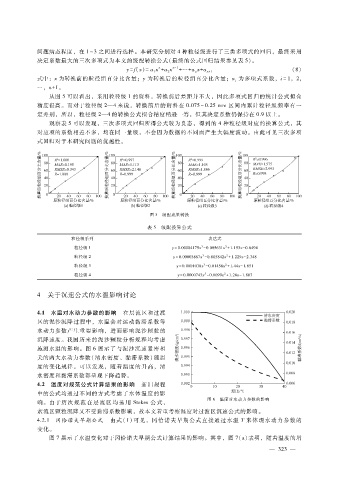
从图 ５可以看出，采用粒径级 １的资料，转换前后差距并不大，因此多项式回归的统计公式拟合
精度很高。而对于粒径级 ２—４来说，转换前后的资料在 ０．０７５～０．２５ｍｍ区间内累计粒径组频率有一
定差别，所以，粒径级 ２—４的转换公式拟合精度稍逊一筹，但其决定系数仍保持在 ０．９以上。
观察表 ５可以发现，三次多项式回归所得公式较为良态，得到的 ４种粒径级对应的换算公式，其
对应项的系数相差不多，均在同一量级，不会因为数据的不同而产生大幅度波动。由此可见三次多项
式回归对于本研究问题的优越性。

图 ５ 级配成果转换
表 ５ 级配换算公式

粒径级系列 表达式
２
３
粒径级 １ ｙ ＝ ０．００００４１７５ｘ－ ０．００５６３１ｘ＋ １．１５３ｘ － ０．６４９４
３
２
粒径级 ２ ｙ ＝ ０ ．００００３８８７ｘ－ ０ ．００５８４２ｘ＋ １ ．２２９ｘ － ２ ．３４８
２
３
粒径级 ３ ｙ ＝ ０ ．０００１０３８ｘ－ ０ ．０１４５８ｘ＋ １ ．４４ｘ － １ ．８５１
２
３
粒径级 ４ ｙ ＝ ０．００００７４３ｘ－ ０．００９９ｘ＋ １．２８ｘ － １．８０７
４ 关于沉速公式的水温影响讨论
４．１ 水温对水动力参数的影响 在层流区和过渡
区的泥沙沉降过程中，水温会对运动黏滞系数等
水动力参数产生重要影响，进而影响泥沙颗粒的
沉降速度。我国历来的泥沙颗粒分析规程均考虑
施测水温的影响。图 ６展示了与泥沙沉速紧密相
关的两大水动力参数（清水密度、黏滞系数）随温
度的变化规律。可以发现，随着温度的升高，清
水密度和黏滞系数都呈现下降趋势。
４．２ 温度对规范公式计算结果的影响 新旧规程
中的公式均通过不同的方式考虑了水体温度的影
图 ６ 温度对水动力参数的影响
响。由于历 次 规 范 在 层 流 区 均 选 用 Ｓｔｏｋｅｓ公 式，
紊流区颗粒沉降又不受黏滞系数影响，故本文着重考察温度对过渡区沉速公式的影响。
４．２．１ 冈恰诺夫早期公式 由式（１）可见，冈恰诺夫早期公式直接通过水温 Ｔ来体现水动力参数的
变化。
图 ７展示了水温变化对于冈恰诺夫早期公式计算结果的影响。其中，图 ７（ａ）表明，随着温度的增
— ３ ２ ３ —