Page 43 - 水利学报2025年第56卷第3期
P. 43
图 8 水温对沙玉清公式的影响
-
ω = ( 13.95 ν ) 2 + 1.09 γ s γ gD- 13.95 ν (9)
槡 D γ D
经过计算得到的分布结果如图 9所示。由图 9(a)表明,随着水温增加,张瑞瑾公式计算的沉速值
同沙玉清公式一样,出现了非线性的增长。这一现象仍可从公式形式本身中寻求解释。张瑞瑾在推导
过渡区的沉速公式时,同时考虑了黏滞阻力和形态阻力的影响,通过求解一个关于沉速的二次方程,
得到了式(9)。这一表达式属于双曲线方程的范畴,因此,在不同的粒径下方程的曲率也不一样。从
而,在刻画粒径变化下非线性乃至非单调的沉速增量值变化成为可能。
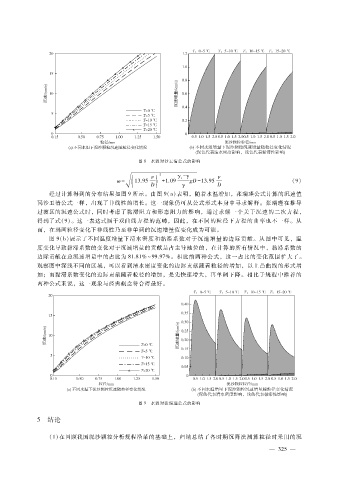
图 9(b)展示了不同温度增量下清水密度和黏滞系数对于沉速增量的边际贡献。从图中可见,温
度变化导致黏滞系数的变化对于沉速增量的贡献是占主导地位的,在计算的所有情况中,黏滞系数的
边际贡献在总沉速增量中的占比为 81.81%~99.97%。相比前两种公式,这一占比的变化范围扩大了。
观察图中深浅不同的区域,可以看到清水密度变化的边际贡献随着粒径的增加,以上凸曲线的形式增
加;而黏滞系数变化的边际贡献随着粒径的增加,是先快速增大,再单调下降。相比于规程中推荐的
两种公式来说,这一现象与经典概念符合得最好。
图 9 水温对张瑞瑾公式的影响
5 结论
(1)在回顾我国泥沙颗粒分析规程沿革的基础上,归纳总结了各时期沉降法测算粒径时采用的沉
— 3 2 5 —